Ángulos correspondientes: una guía práctica.
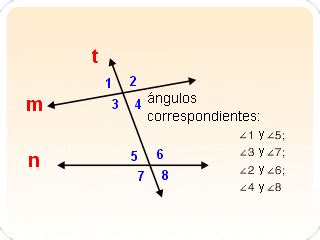
En geometría, los ángulos correspondientes son un concepto fundamental que se utiliza para comprender y analizar diversas figuras y formas. Estos ángulos desempeñan un papel crucial en la identificación de simetrías y relaciones entre figuras, lo que permite realizar análisis más profundos y precisos en diferentes ramas de la matemática y la ciencia.
Definición y Características de los Ángulos Correspondientes
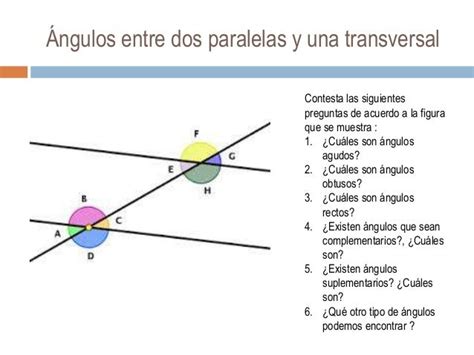
Los ángulos correspondientes se definen como aquellos ángulos que ocupan la misma posición o lugar en dos figuras geométricas congruentes. Estas figuras congruentes pueden ser polígonos, triángulos, rectángulos, o cualquier otra figura geométrica que posea una simetría o relación de transformación entre sí.
Los ángulos correspondientes siempre se encuentran en posiciones equivalentes en ambas figuras. Por ejemplo, si tenemos dos triángulos congruentes, el ángulo correspondiente a un vértice específico en uno de los triángulos será el ángulo en la misma posición del otro triángulo. Esta correspondencia es lo que nos permite establecer relaciones entre las figuras y extraer conclusiones sobre sus propiedades.
Propiedades y Aplicaciones de los Ángulos Correspondentes
Los ángulos correspondientes poseen varias propiedades interesantes que son útiles en diversos contextos:
- Congruencia: Los ángulos correspondientes son congruentes entre sí. Esto significa que tienen la misma medida angular. Por ejemplo, si dos triángulos son congruentes, el ángulo correspondiente a un vértice específico en uno de los triángulos tendrá la misma medida que el ángulo correspondiente en el otro triángulo.
- Simetría: La existencia de ángulos correspondientes indica una simetría entre las figuras. Esta simetría puede ser de reflejo, rotación, o una combinación de ambas. La identificación de ángulos correspondientes nos ayuda a reconocer y analizar estas simetrías.
- Teorema de los Ángulos Internos: En polígonos convexos, la suma de los ángulos internos de un polígono es igual a la suma de los ángulos internos de cualquier otro polígono congruente. Esto significa que los ángulos correspondientes en polígonos congruentes también tienen la misma suma.
- Aplicaciones en Triángulos: En el caso de triángulos, los ángulos correspondientes son particularmente útiles para demostrar la congruencia de triángulos. Por ejemplo, si se pueden identificar cuatro pares de ángulos correspondientes congruentes en dos triángulos, se puede concluir que los triángulos son congruentes.
| Figura Geométrica | Ángulos Correspondientes |
|---|---|
| Triángulo Rectángulo | Los ángulos correspondientes a los vértices del triángulo recto. |
| Rectángulo | Los ángulos correspondientes en las esquinas opuestas del rectángulo. |
| Pentágono Regular | Los ángulos correspondientes en cada vértice del pentágono. |

Identificación y Comparación de Ángulos Correspondientes

La identificación de ángulos correspondientes es un proceso crucial para comprender y analizar figuras geométricas. En general, para identificar ángulos correspondientes, se deben seguir los siguientes pasos:
- Identificación de Figuras Congruentes: Lo primero es identificar dos figuras geométricas que sean congruentes. Esto significa que deben tener la misma forma y tamaño. Las figuras congruentes pueden ser polígonos, triángulos, rectángulos, u otras formas.
- Selección de Ángulos: Una vez identificadas las figuras congruentes, se seleccionan los ángulos que se desean comparar. Estos ángulos deben estar en posiciones equivalentes en ambas figuras.
- Medición y Comparación: Se miden los ángulos seleccionados y se comparan sus medidas. Si los ángulos correspondientes tienen la misma medida, esto indica que son congruentes y que las figuras en cuestión poseen una relación de simetría o congruencia.
La comparación de ángulos correspondientes no solo es útil para determinar la congruencia de figuras, sino que también puede ser utilizada para demostrar teoremas geométricos y resolver problemas complejos. Por ejemplo, en el caso de triángulos, si se pueden identificar ángulos correspondientes congruentes, se puede utilizar el Teorema de los Ángulos Congruentes para demostrar que los triángulos son congruentes.
Aplicaciones Prácticas
Los ángulos correspondientes tienen una amplia gama de aplicaciones prácticas en diversas áreas:
- Arquitectura y Construcción: En la arquitectura y la construcción, los ángulos correspondientes son esenciales para asegurar la estabilidad y simetría de las estructuras. Los arquitectos y constructores utilizan ángulos correspondientes para diseñar edificios y puentes con una distribución equilibrada de fuerzas.
- Ingeniería Mecánica: En la ingeniería mecánica, los ángulos correspondientes se aplican en el diseño de máquinas y mecanismos. La identificación de ángulos correspondientes permite a los ingenieros asegurar que las partes mecánicas se ajusten correctamente y funcionen de manera eficiente.
- Robótica y Automatización: En el campo de la robótica y la automatización, los ángulos correspondientes son cruciales para la programación y el control de robots. Los robots utilizan sensores y algoritmos para identificar y ajustar ángulos correspondientes en su entorno, permitiendo una navegación precisa y la manipulación de objetos.
- Medicina e Imagenología: En medicina, especialmente en la imagenología, los ángulos correspondientes se utilizan en técnicas como la tomografía computarizada (TC) y la resonancia magnética (RM). Estas técnicas utilizan ángulos correspondientes para crear imágenes precisas del cuerpo humano, permitiendo a los médicos diagnosticar y tratar diversas condiciones.
Ángulos Correspondientes en Triángulos y Polígonos
Los ángulos correspondientes son particularmente importantes en la geometría de triángulos y polígonos. En estas figuras, los ángulos correspondientes desempeñan un papel clave en la demostración de la congruencia y la igualdad de medidas.
Ángulos Correspondientes en Triángulos
En el caso de triángulos, los ángulos correspondientes son esenciales para demostrar la congruencia de triángulos. Si se pueden identificar cuatro pares de ángulos correspondientes congruentes en dos triángulos, se puede concluir que los triángulos son congruentes. Esta propiedad es conocida como el Criterio de Congruencia de Triángulos.
Además, en triángulos isósceles y escalenos, los ángulos correspondientes tienen una relación especial. En un triángulo isósceles, los ángulos correspondientes a los lados iguales son congruentes. En un triángulo escaleno, los ángulos correspondientes a los lados desiguales también son congruentes.
Ángulos Correspondientes en Polígonos
En polígonos convexos, la suma de los ángulos internos de un polígono es igual a la suma de los ángulos internos de cualquier otro polígono congruente. Esto significa que los ángulos correspondientes en polígonos congruentes también tienen la misma suma. Esta propiedad es conocida como el Teorema de los Ángulos Internos de Polígonos Convexos.
En polígonos regulares, como el pentágono, hexágono, o octágono, los ángulos correspondientes son iguales entre sí. Esto se debe a que todos los ángulos internos de un polígono regular son congruentes. Por ejemplo, en un pentágono regular, todos los ángulos internos son iguales y corresponden entre sí.
Aplicaciones Avanzadas y Futuro de los Ángulos Correspondientes
Los ángulos correspondientes tienen aplicaciones avanzadas en diversos campos de la ciencia y la tecnología. En la robótica, por ejemplo, los ángulos correspondientes son utilizados para la navegación y la percepción espacial de los robots. Los algoritmos de visión artificial y procesamiento de imágenes utilizan ángulos correspondientes para identificar objetos y orientar robots en entornos complejos.
En el futuro, se espera que los ángulos correspondientes continúen siendo una herramienta esencial en la geometría y la matemática. Con el avance de la tecnología y la computación, se están desarrollando algoritmos y técnicas avanzadas para la identificación y análisis de ángulos correspondientes en figuras geométricas complejas. Estas herramientas permitirán a los científicos y matemáticos resolver problemas más complejos y explorar nuevas áreas de la geometría.
Además, la aplicación de ángulos correspondientes en la vida cotidiana y en diversas industrias continuará evolucionando. En el campo de la medicina, por ejemplo, se están desarrollando técnicas de imagenología avanzadas que utilizan ángulos correspondientes para crear imágenes detalladas del cuerpo humano. Estas imágenes permiten a los médicos diagnosticar y tratar enfermedades con mayor precisión y eficacia.
¿Cómo se determinan los ángulos correspondientes en figuras complejas?
+En figuras complejas, como curvas o figuras irregulares, la determinación de ángulos correspondientes puede ser más desafiante. En estos casos, se utilizan técnicas avanzadas de geometría diferencial y topología para identificar ángulos correspondientes. Estas técnicas implican el uso de herramientas matemáticas sofisticadas para analizar la estructura y simetría de las figuras.
¿Qué aplicaciones tienen los ángulos correspondientes en la vida cotidiana?
+Los ángulos correspondientes tienen diversas aplicaciones en la vida cotidiana. Por ejemplo, en la construcción de edificios, los arquitectos utilizan ángulos correspondientes para asegurar la estabilidad y simetría de las estructuras. En la imagenología médica, los ángulos correspondientes son utilizados para crear imágenes detalladas del cuerpo humano, permitiendo a los médicos diagnosticar y tratar enfermedades.
¿Cuál es la importancia de los ángulos correspondientes en la matemática avanzada?
+En la matemática avanzada, los ángulos correspondientes son fundamentales para el estudio de la geometría y la topología. Estos ángulos permiten a los matemáticos analizar y comprender la estructura y simetría de figuras geométricas complejas. Además, los ángulos correspondientes son utilizados en diversas áreas de la matemática, como la teoría de grupos y la geometría algebraica.



