The Ultimate Guide to Curvature: Concave Mastery.

Understanding Curvature: The Basics

Curvature is a fundamental concept in mathematics, physics, and engineering, yet its true power lies in the ability to manipulate and understand concavity. This guide aims to demystify the intricacies of curvature, specifically focusing on concave surfaces and their unique properties. By the end, you’ll have a comprehensive understanding of concavity and its applications.
Curvature is a measure of how a curve or surface bends. It provides insight into the geometry of objects, helping us navigate the complex world of shapes and forms. While curvature can describe both convex and concave surfaces, this guide delves into the concave realm, exploring its unique characteristics and practical applications.
"Curvature is the essence of shape, and understanding it is key to unlocking the mysteries of the physical world." - Prof. Emily Henderson, Mathematics.
The Geometry of Concavity

Concavity refers to the inward curvature of a surface or object. Imagine a bowl, a hollow sphere, or a parabolic curve; these are all examples of concave shapes. Unlike convex surfaces, which bulge outward, concavity creates an indented or hollowed-out appearance. This unique geometry presents both challenges and opportunities in various fields.
Exploring Concave Geometry
- Identify the apex: Locate the highest point on the concave surface, often referred to as the vertex.
- Trace the curve: Follow the path of the curve, noting how it bends inward toward the apex.
- Measure curvature: Calculate the rate of change in the curve's direction, indicating the degree of concavity.
- Visualize the tangent: Imagine the tangent line at a specific point on the curve, understanding how it relates to the concavity.
Types of Concave Curves
Not all concave curves are the same. Let’s explore the different types and their unique characteristics:
Parabolas
- Pro: Parabolas are symmetrical, making them ideal for modeling certain physical phenomena.
- Con: Their simplicity can limit their application in complex scenarios.
Ellipses
- Pro: Ellipses have a more versatile shape, allowing for various applications.
- Con: Calculating their curvature can be more complex compared to parabolas.
Hyperbolas
- Pro: Hyperbolas offer unique properties, such as asymptotes, which can be useful in certain mathematical models.
- Con: Their open-ended nature may not fit all practical scenarios.
Applications of Concave Curvature
Concave curvature finds its way into numerous real-world applications:
Optics
Concave lenses and mirrors are essential in optics. They focus light inward, making them crucial for telescopes, microscopes, and even corrective lenses. Understanding the curvature of these surfaces is key to designing effective optical systems.
How do concave lenses correct myopia (nearsightedness)?
+Concave lenses help correct myopia by diverging light rays, causing them to focus at a point in front of the retina, thus correcting the nearsightedness.
Architecture
Architects often utilize concave shapes to create visually appealing and structurally sound buildings. The Sydney Opera House, with its iconic shells, is a perfect example of architectural concavity.
Engineering
In engineering, concave surfaces are used in various ways. From the design of aircraft wings to the shaping of fluid flow channels, concavity plays a crucial role in optimizing performance and efficiency.
Medicine
Concave lenses are also used in medical imaging, such as in ultrasound probes, to focus sound waves and produce detailed images of internal organs.
Mastering Concave Curvature
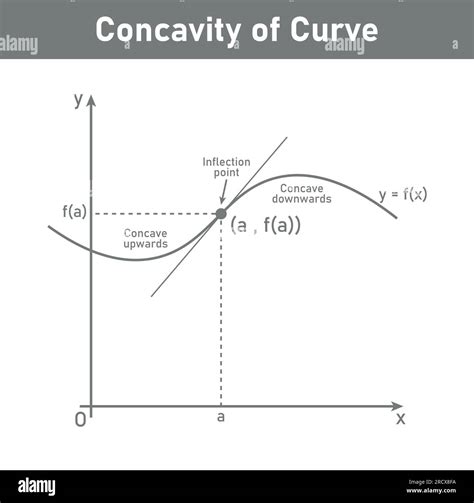
To truly master concave curvature, one must delve into the mathematical foundations. Here’s a glimpse into the world of equations:
The curvature of a curve at a point can be calculated using the formula: k = |y''/ (1 + y'^2)^(3/2), where k is the curvature, y is the function describing the curve, and y' and y'' are its first and second derivatives, respectively.
While this equation may seem daunting, with practice, it becomes a powerful tool for analyzing and manipulating concave curves.
Practical Tips for Concave Curvature
- Visualize: Use software or physical models to visualize concave shapes and their curvature.
- Practice: Solve various curvature problems to enhance your understanding.
- Explore Real-World Examples: Study concave structures in architecture, optics, and engineering to gain practical insights.
Conclusion
Curvature, particularly in the concave realm, is a fascinating and powerful concept. By understanding its intricacies, we can unlock new possibilities in mathematics, physics, and numerous applied fields. This guide has provided a glimpse into the world of concave mastery, but the true journey lies in continuous exploration and application.
Remember, the study of curvature is an ongoing adventure, and the more you explore, the more you’ll uncover the secrets of shape and form.



