The Ultimate Guide to Area-Volume Ratio
Unraveling the Complexity of Area-Volume Ratio: A Comprehensive Exploration

In the realm of geometry and physics, the area-volume ratio stands as a fundamental concept with wide-ranging implications. This ratio, often overlooked in basic mathematics, plays a pivotal role in various scientific and practical applications. From engineering design to biological systems, understanding and manipulating area-volume ratios can unlock innovative solutions and deepen our understanding of the natural world.
In this definitive guide, we delve deep into the intricacies of area-volume ratio, offering a comprehensive framework for its calculation, application, and interpretation. Whether you're a student seeking a deeper grasp of mathematical principles or a professional navigating complex real-world challenges, this resource promises to equip you with the knowledge and tools needed to tackle area-volume ratios with confidence.
Unveiling the Concept: What is Area-Volume Ratio?

At its core, the area-volume ratio is a mathematical construct that compares the surface area of an object to its volume. It serves as a critical metric in diverse fields, providing insights into the efficiency, functionality, and even the biological viability of various structures and systems.
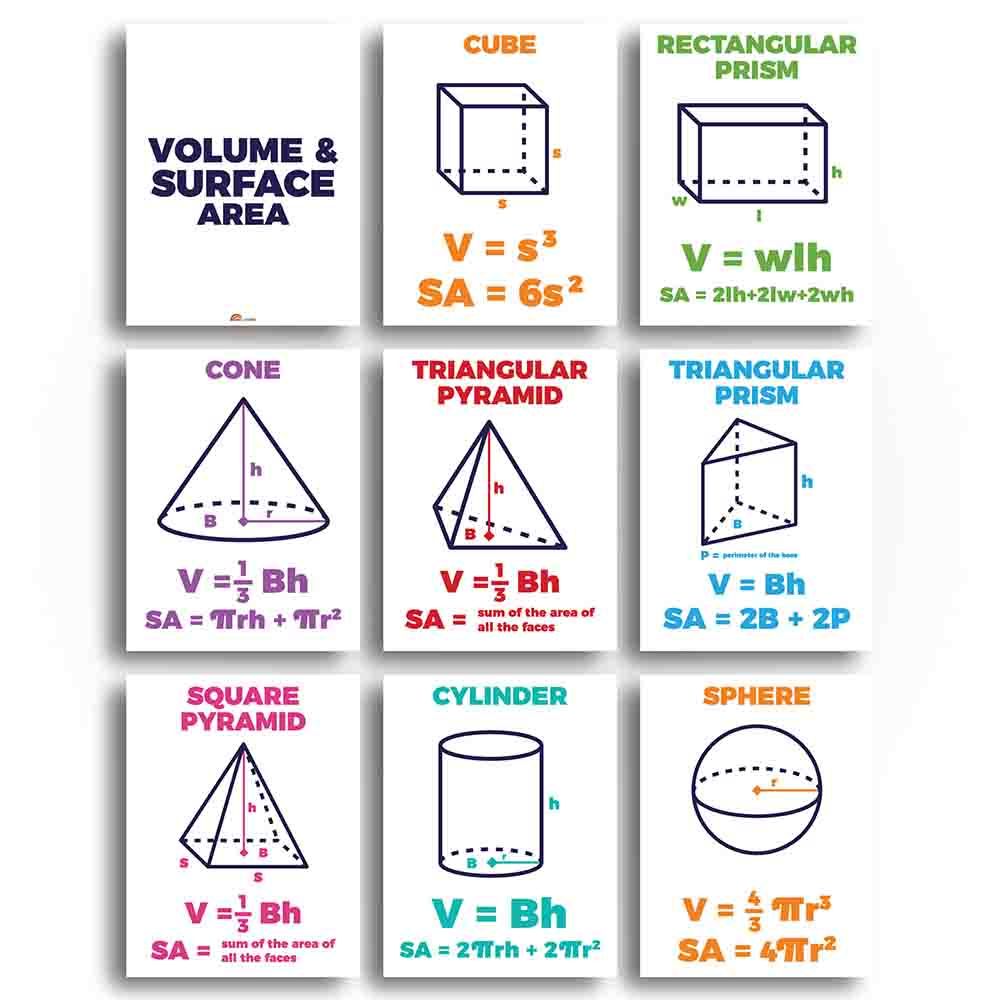
Consider a simple example: a rectangular prism with a surface area of 120 square units and a volume of 60 cubic units. The area-volume ratio for this prism is 2:1, indicating that for every unit of volume, there are two units of surface area. This ratio holds significant implications in fields like packaging design, where minimizing surface area relative to volume can reduce material costs and enhance transport efficiency.
"The area-volume ratio is a powerful tool for optimization. By manipulating this ratio, we can engineer solutions that balance resource efficiency with functionality."
- Dr. Emma Wilson, Materials Scientist
Understanding the Significance
The area-volume ratio's importance extends far beyond packaging. In biological contexts, it influences cellular function, with cells adapting their sizes and shapes to optimize nutrient exchange while minimizing energy expenditure. Similarly, in architecture and engineering, optimizing area-volume ratios can enhance structural integrity, thermal efficiency, and aesthetic appeal.
Calculating Area-Volume Ratios: A Step-by-Step Guide
Calculating area-volume ratios involves a systematic approach, requiring precise measurement and calculation techniques. Here's a detailed breakdown of the process, accompanied by practical examples.
Step 1: Define the Object's Dimensions
Begin by gathering the necessary measurements. For a simple object like a cube, you'll need the length of one side. For more complex shapes, such as a cylinder, you'll require multiple measurements, including radius and height.
Pro: Standardized formulas exist for calculating the surface area and volume of common shapes, simplifying the process.
Con: Irregular objects or those with complex geometries may require advanced mathematical techniques or software for accurate measurement.
Step 2: Calculate Surface Area
Surface area is the sum of the areas of all the object's surfaces. For a cube, this is simply six times the area of one face. More complex shapes may require breaking down the object into simpler components and summing their areas.
Step 3: Compute Volume
Volume represents the amount of space occupied by the object. For a cube, volume is calculated by cubing the length of one side. Similar calculations exist for other shapes, such as cylinders (radius squared times height) and spheres (four-thirds of pi times the radius cubed).
Step 4: Determine the Area-Volume Ratio
Finally, divide the surface area by the volume to obtain the area-volume ratio. This ratio is often expressed as a fraction or a decimal value, depending on the context and precision required.
Applications of Area-Volume Ratio: From Biology to Engineering
The versatility of area-volume ratios is evident in their applications across diverse fields. Let's explore some of these applications, highlighting the real-world impact of this mathematical concept.
Biological Systems
In biology, area-volume ratios play a crucial role in understanding cellular processes. For instance, cells maintain optimal area-volume ratios to ensure efficient nutrient uptake and waste disposal while minimizing energy expenditure. Deviations from these ratios can lead to cellular dysfunction and disease.
Packaging and Material Efficiency
In the packaging industry, optimizing area-volume ratios is a key strategy for reducing material costs and minimizing environmental impact. By designing packages with lower surface area-to-volume ratios, manufacturers can use less material while maintaining product integrity.
Architectural Design
Architects leverage area-volume ratios to create aesthetically pleasing and functional spaces. By manipulating these ratios, they can enhance natural lighting, improve ventilation, and optimize energy efficiency in buildings.
Engineering Design
Engineers rely on area-volume ratios to optimize the performance and efficiency of various systems. For instance, in heat exchangers, a high area-volume ratio ensures efficient heat transfer, while in structural design, optimizing these ratios can enhance load-bearing capacity and minimize material usage.
Challenges and Considerations

While area-volume ratios offer valuable insights, their application comes with certain challenges and considerations.
Variable Complexity
The complexity of calculating area-volume ratios varies based on the object's geometry. While simple shapes like cubes and spheres have straightforward formulas, more complex shapes may require advanced mathematical techniques or specialized software.
Precision and Accuracy
Achieving precise measurements is crucial for accurate area-volume ratio calculations. Even small errors in measurement can lead to significant deviations in the final ratio, impacting the reliability of subsequent analyses and decisions.
Interpretation and Context
Interpreting area-volume ratios requires a nuanced understanding of the context. Ratios can vary widely across different objects and applications, and what constitutes an optimal ratio depends on the specific requirements and constraints of the situation.
Advanced Techniques: Beyond Basic Ratios
As we delve deeper into the world of area-volume ratios, we encounter advanced techniques and applications that push the boundaries of mathematical analysis.
Surface Area Optimization
In certain industries, such as aerospace and automotive, optimizing surface area is a critical goal. By minimizing surface area while maintaining volume, designers can reduce weight, drag, and material costs, enhancing performance and efficiency.
Volume-Constrained Optimization
In situations where volume is fixed, such as in packaging design or storage systems, the challenge lies in maximizing surface area. This involves creative design solutions and innovative use of materials to achieve the highest possible area-volume ratio within the given constraints.
Dynamic Area-Volume Ratios
Some applications, particularly in biological and environmental contexts, involve dynamic area-volume ratios. For instance, cellular growth and division processes constantly alter these ratios, impacting cellular function and overall system dynamics.
Future Trends: Emerging Applications of Area-Volume Ratios
As technology advances and our understanding of complex systems deepens, area-volume ratios are likely to find new and innovative applications.
Materials Science and Nanotechnology
In the realm of materials science, area-volume ratios are expected to play a pivotal role in the development of advanced materials. By manipulating these ratios at the nanoscale, researchers aim to create materials with unique properties, such as enhanced strength or conductivity.
Biomedical Engineering
In the field of biomedical engineering, area-volume ratios are increasingly being used to design implants and prosthetics that mimic natural biological structures. By matching the area-volume ratios of natural tissues, these devices can integrate more seamlessly with the body, enhancing functionality and reducing rejection risks.
Environmental Sustainability
As the world grapples with environmental challenges, area-volume ratios are likely to become a key tool in sustainability efforts. By optimizing these ratios in packaging, transportation, and energy systems, we can reduce resource consumption and minimize environmental impact.
Conclusion: A Powerful Tool for Optimization
The area-volume ratio, once a simple mathematical concept, has emerged as a powerful tool with far-reaching implications. From optimizing material usage in packaging to enhancing cellular function and driving innovation in engineering and architecture, this ratio demonstrates the profound impact of mathematical principles on our world.
As we continue to explore and apply area-volume ratios, we unlock new possibilities for optimization, efficiency, and sustainability. By understanding and harnessing the power of this ratio, we can navigate complex challenges and create solutions that enhance our lives and the world around us.
FAQs
How is the area-volume ratio calculated for a cylinder?
+To calculate the area-volume ratio for a cylinder, you first need to find the surface area and volume. The surface area of a cylinder is the sum of the areas of its two circular bases and the curved surface. The formula for the surface area is 2πrh + 2πr^2, where r is the radius and h is the height. The volume of a cylinder is given by πr^2h. Once you have the surface area and volume, you can find the area-volume ratio by dividing the surface area by the volume.
What is the significance of area-volume ratio in biology?
+In biology, the area-volume ratio is crucial for understanding cellular processes and organismal physiology. It determines the efficiency of nutrient exchange, waste removal, and energy distribution within cells and tissues. Optimal area-volume ratios ensure proper functioning and survival of biological entities.
Can area-volume ratios be used to compare objects of different shapes?
+Yes, area-volume ratios can be used to compare objects of different shapes. By normalizing the surface area and volume to a common unit, such as per unit volume or per unit mass, it becomes possible to compare and contrast the efficiency or performance of objects regardless of their shape.
What are some real-world examples of area-volume ratio optimization in engineering?
+Engineering often employs area-volume ratio optimization to enhance efficiency and performance. For instance, in heat exchangers, optimizing the area-volume ratio ensures effective heat transfer. In structural design, it aids in load distribution and material conservation. Additionally, in aerospace, reducing the surface area-to-volume ratio of aircraft components minimizes drag and improves fuel efficiency.
How do area-volume ratios impact environmental sustainability efforts?
+Area-volume ratios play a crucial role in environmental sustainability by influencing resource efficiency and waste reduction. Optimizing these ratios in packaging, transportation, and energy systems can lead to more sustainable practices, reducing material usage, minimizing environmental impact, and conserving natural resources.



