5 Easy Steps: Disc Method Formula

Step 1: Understand the Problem

Before diving into the Disc Method, it’s crucial to grasp the essence of the problem at hand. Take a moment to analyze the given information and identify the key elements. Understanding the problem is the foundation upon which the entire solution is built.

For instance, imagine you’re faced with a disc that has a radius of 5 units and a height of 3 units. Your task is to find the volume of this disc-shaped object. By recognizing the dimensions and the nature of the object, you’re already one step closer to finding the solution.

Step 2: Visualize the Disc

Visualization is a powerful tool in mathematics. It allows us to make sense of abstract concepts and simplifies the problem-solving process. In the case of the Disc Method, visualizing the disc is essential.

Consider the disc as a three-dimensional object with a curved surface. Imagine holding this disc in your hand and rotating it to examine its shape from different angles. This visualization step helps in understanding the spatial relationships within the disc.

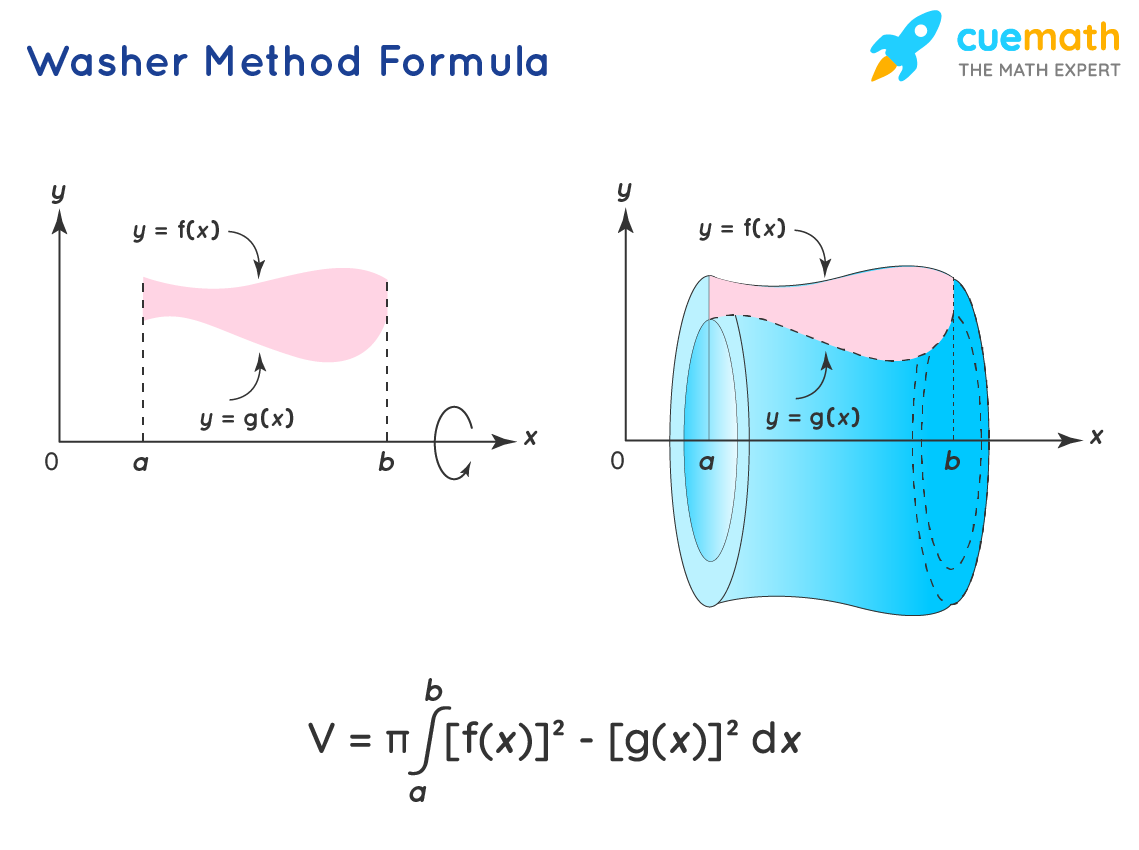
Step 3: Apply the Disc Method Formula

Now, it’s time to bring the Disc Method Formula into play. The formula is a mathematical expression that encapsulates the relationship between the dimensions of the disc and its volume. It looks like this:

\[ \begin{equation*} V = \frac{\pi \cdot r^2 \cdot h}{3} \, . \end{equation*} \]

Here, V represents the volume of the disc, \pi is a mathematical constant approximately equal to 3.14159, r is the radius of the disc, and h is the height.

By plugging in the given values into the formula, you can calculate the volume of the disc. For our example, with a radius of 5 units and a height of 3 units, the calculation would be:

\[ \begin{align*} V &= \frac{\pi \cdot (5 \text{ units})^2 \cdot (3 \text{ units})}{3} \\ &= \frac{25 \pi \text{ units}^3}{3} \, . \end{align*} \]

Step 4: Interpret the Result

Once you’ve obtained the numerical result, it’s important to interpret its meaning in the context of the problem. In our case, the result \frac{25 \pi \text{ units}^3}{3} represents the volume of the disc.

However, it’s worth noting that the result contains the value of \pi, which is an irrational number. This means the volume cannot be expressed as a simple fraction or decimal. It highlights the precision and complexity of the Disc Method Formula.

Step 5: Apply the Solution

The final step is to apply the solution to the problem at hand. In our disc volume example, the calculated volume can be used in various real-world scenarios.

For instance, if you’re designing a storage container in the shape of a disc, knowing its volume helps in determining the capacity of the container. It can also be applied in engineering projects, such as calculating the volume of a cylindrical tank or a disc-shaped aircraft part.

Expert Perspective: Real-World Applications

Practical Application Guide: Designing a Disc-Shaped Water Tank

Imagine you’re tasked with designing a water tank in the shape of a disc for a remote village. The Disc Method Formula can be a valuable tool in this scenario. By following these steps:

1. Determine the required water capacity and convert it into a volume measurement.
2. Calculate the necessary radius and height of the disc using the Disc Method Formula.
3. Design the tank’s structure, considering factors like material strength and ease of construction.
4. Test the tank’s performance and ensure it meets the village’s water needs.

Future Implications: Advancements in Disc Method Calculations

As technology advances, so do the tools available for mathematical calculations. The future of the Disc Method Formula may involve the integration of advanced computational software and artificial intelligence. These developments could streamline the calculation process and provide even more precise results.

FAQ Section

    <div class="faq-item">
        <div class="faq-question">
            <h3>Can the Disc Method be used for objects other than discs?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>While the Disc Method is specifically designed for disc-shaped objects, similar mathematical formulas exist for other shapes. For instance, the Cylinder Method is used for cylindrical objects, and the Sphere Method for spherical objects. Each formula is tailored to the unique characteristics of its respective shape.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>Are there any limitations to the Disc Method Formula's applicability?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>The Disc Method Formula assumes a perfect disc shape with uniform dimensions. In real-world scenarios, objects may have variations or imperfections. These irregularities can affect the accuracy of the formula. Additionally, the formula is not applicable to objects with complex shapes or multiple dimensions.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>How can I improve my understanding of the Disc Method Formula?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Practicing with a variety of disc-shaped objects and real-world scenarios is key to improving your understanding. Try applying the formula to different shapes and sizes, and compare the results with expected values. Online tutorials and educational resources can also provide valuable insights and help solidify your knowledge.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>Is the Disc Method Formula applicable to all mathematical disciplines?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>The Disc Method Formula is primarily used in geometry and calculus, particularly in the study of three-dimensional shapes. While it has specific applications in these disciplines, it may not be directly applicable to other areas of mathematics such as algebra or number theory.</p>
        </div>
    </div>

</div>