3 Ways to Master Interval Notation
Understanding Interval Notation: A Key Skill for Mathematical Precision

Interval notation is a powerful tool in mathematics, offering a concise and precise way to represent sets of numbers. This skill is essential for anyone looking to navigate the world of mathematics with ease and confidence. By mastering interval notation, you gain a deeper understanding of mathematical concepts and the ability to communicate ideas clearly.
Here, we’ll explore three effective strategies to help you become an expert in interval notation, enabling you to tackle complex mathematical problems with efficiency and accuracy.
1. Visualizing Intervals: A Picture is Worth a Thousand Words
One of the most effective ways to grasp interval notation is by visualizing it. Think of intervals as regions on a number line, each with a unique range of values. By associating intervals with visual representations, you can develop a strong intuitive understanding of their boundaries and characteristics.
Imagine interval notation as a map guiding you through the vast landscape of numbers. Each interval is like a distinct territory, with its own rules and boundaries.
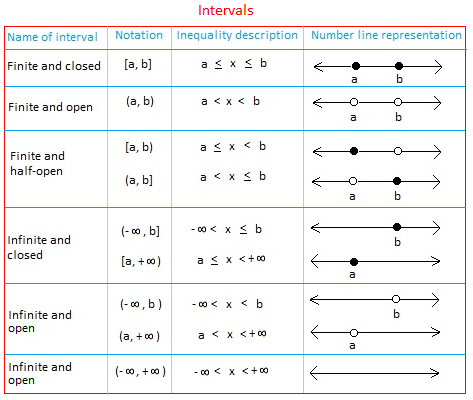
Let’s consider a simple example: the interval [3, 7]. This notation represents all the numbers between 3 and 7, including 3 and 7 themselves. By visualizing this interval on a number line, you can see it as a closed region, indicated by the square brackets. On the other hand, the interval (3, 7) would represent an open region, excluding both 3 and 7, as indicated by the parentheses.
- Start by drawing a number line and marking the endpoints of your interval.
- Use different symbols for open and closed endpoints to differentiate them.
- Color-code or shade the region representing your interval for better visualization.
- Practice with various intervals, gradually increasing their complexity.
Through visualization, you can quickly identify the nature of an interval, whether it’s open, closed, or semi-open, and understand its position relative to other intervals. This visual approach not only makes learning interval notation more engaging but also helps in retaining the knowledge for longer.
2. Mastering the Language of Interval Notation
Interval notation has its own unique language, with specific symbols and conventions that convey precise mathematical meanings. By familiarizing yourself with this language, you can communicate mathematical ideas clearly and understand others’ expressions effortlessly.
| Symbol | Meaning |
|---|---|
| [ ] | Closed interval, includes endpoints |
| ( ) | Open interval, excludes endpoints |
| [ ) | Left-closed, right-open interval |
| ( ] | Left-open, right-closed interval |

In addition to these basic symbols, interval notation also involves understanding how to represent unbounded intervals, such as (-∞, 5) for all numbers less than 5, and (3, ∞) for all numbers greater than 3.
Pro: Standardized language for clear communication.
Con: Requires memorization and practice to master.
To become proficient in this language, practice is key. Work through various examples, identifying the interval boundaries and their associated symbols. Over time, you’ll develop a natural fluency in interpreting and expressing intervals accurately.
3. Applying Interval Notation in Real-World Scenarios
The true test of mastering any skill is its application in practical situations. Interval notation is no exception. By applying your knowledge of interval notation to real-world problems, you reinforce your understanding and develop problem-solving skills.
Consider the following scenario: you’re working on a project that involves analyzing temperature data. The data represents the daily maximum temperatures for a particular region over a month. Your task is to identify the days when the temperature exceeded 30°C but did not reach 40°C.
Using interval notation, you can represent this situation as (30, 40). By visualizing this interval on a number line, you can easily identify the desired temperature range and interpret the data accordingly.
Real-world application reinforces theoretical knowledge, making it more meaningful and memorable.
Interval notation finds applications in various fields, from physics and engineering to economics and statistics. By practicing its use in diverse contexts, you’ll develop a versatile skill set that will serve you well throughout your academic and professional journey.
Conclusion: Unlocking the Power of Interval Notation

Mastering interval notation is a journey that requires practice, visualization, and real-world application. By embracing these strategies, you’ll not only enhance your mathematical skills but also develop a deeper appreciation for the beauty and precision of mathematics.
Remember, interval notation is a powerful tool that empowers you to communicate complex ideas with clarity and precision. With dedication and a willingness to explore, you can unlock its full potential and become an expert in this essential mathematical skill.
What is interval notation, and why is it important in mathematics?
+Interval notation is a concise way to represent sets of numbers in mathematics. It provides a standardized method for expressing ranges of values, which is crucial for solving complex mathematical problems, analyzing data, and communicating mathematical ideas effectively.
How do I know when to use square brackets and when to use parentheses in interval notation?
+Square brackets ([ ]) indicate that the endpoint values are included in the interval. Parentheses ( ) indicate that the endpoint values are not included. This distinction is crucial for precise mathematical communication and analysis.
Can interval notation represent unbounded intervals, and how do I write them?
+Yes, interval notation can represent unbounded intervals. For negative infinity, we use the symbol -∞, and for positive infinity, we use ∞. For example, (-∞, 5) represents all numbers less than 5, and (3, ∞) represents all numbers greater than 3.
How does interval notation help in real-world problem-solving, especially in data analysis?
+Interval notation provides a clear and precise way to define and analyze data ranges. In data analysis, it helps identify patterns, trends, and outliers within specific intervals. This makes it an essential tool for making informed decisions based on data.