How to Calculate a Rectangle's Perimeter
Let’s dive into the world of geometry and explore the simple yet essential concept of calculating a rectangle’s perimeter. Understanding this is crucial for various applications, from architecture and engineering to everyday measurements. So, let’s get started!
The Fundamental Concept

A rectangle is a four-sided shape with four right angles, and its perimeter refers to the total distance around its outer boundary. To calculate this, we need to find the sum of the lengths of all its sides.
Mathematical Formula

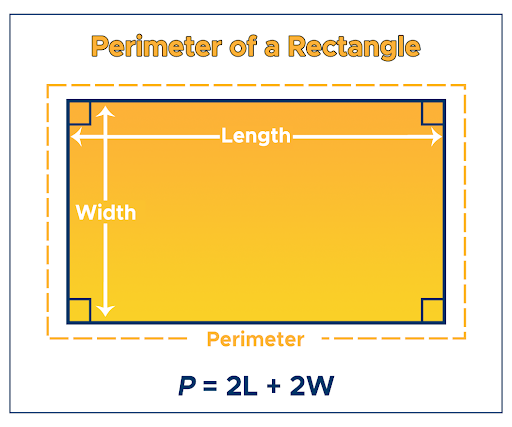
The formula for finding a rectangle’s perimeter is straightforward:
Perimeter = 2 * (Length + Width)
Here, ‘Length’ represents the longer side of the rectangle, and ‘Width’ refers to the shorter side. This formula is derived from the basic principle that a rectangle has two pairs of equal-length sides, so adding the lengths of all four sides gives us the perimeter.
Step-by-Step Guide
Now, let’s break down the process of calculating a rectangle’s perimeter with a practical example:
Scenario: Imagine you have a rectangular garden, and you want to install a fence around it. The length of the garden is 12 meters, and the width is 8 meters. How do you find the perimeter to determine the total length of fencing required?
Solution:
Step 1: Identify the Length and Width: As mentioned, the length is 12 meters, and the width is 8 meters.
Step 2: Apply the Formula: Plug these values into the formula: Perimeter = 2 * (12 + 8).
Step 3: Calculate: Performing the multiplication first, we get: Perimeter = 2 * 20. Then, multiplying 2 by 20 gives us: Perimeter = 40.
So, the perimeter of this rectangular garden is 40 meters, which is the total length of fencing needed to enclose it.
Practical Applications
Understanding how to calculate a rectangle’s perimeter has numerous practical applications:
- Construction: Architects and builders use this calculation to determine the amount of fencing, piping, or wiring required for various projects.
- Landscaping: Gardeners and landscape designers can use it to plan the layout of paths, fences, or flower beds.
- Geometric Analysis: In mathematics, understanding perimeters is fundamental for more complex geometric concepts and proofs.
- Everyday Life: It’s useful for everyday tasks like measuring the length of a room for flooring or determining the length of a fence for a backyard.
Visual Representation

To further illustrate this concept, here’s a simple diagram of a rectangle with its sides labeled:

A rectangle with length 12 units and width 8 units, showing the formula for perimeter: Perimeter = 2 * (12 + 8) = 40 units.
Variations and Complex Scenarios
While the formula provided works for most basic rectangular shapes, there are variations to consider:
- Square: A square is a special type of rectangle with all four sides equal in length. In this case, the formula simplifies to Perimeter = 4 * Side Length.
- Irregular Rectangles: For more complex shapes, like rectangles with different lengths for each pair of opposite sides, you’d calculate the sum of all four sides separately.
Pro Tip
Always measure the length and width of a rectangle accurately to ensure precise calculations. Even small discrepancies can lead to significant errors in the perimeter calculation, especially for larger rectangles.
Final Thoughts
Understanding how to calculate a rectangle’s perimeter is a fundamental skill with broad applications. Whether you’re a student learning geometry, a professional in a field that utilizes geometric principles, or simply someone facing a practical measurement task, this knowledge is invaluable.
So, the next time you encounter a rectangle, whether it’s on paper or in the real world, you’ll know exactly how to find its perimeter!



