Unraveling Fractions: Numerator and Denominator
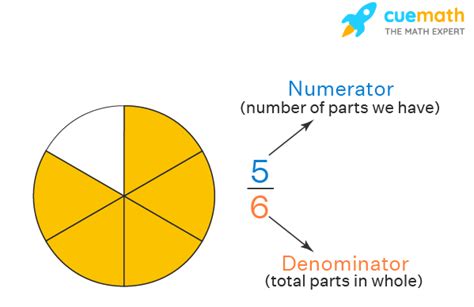
Numerators and denominators are the building blocks of fractions, serving as essential components that define the quantity and proportion represented by a fraction. Their relationship and understanding are fundamental to working with fractions effectively.
Understanding the Role of Numerators
The numerator sits above the line in a fraction, indicating the number of parts being considered. It represents a specific quantity, which could be a whole number or a fraction itself. The numerator defines the magnitude or extent of the fraction. For example, in the fraction 3⁄4, the numerator 3 signifies three parts out of four.
Denominators: Defining the Whole
The denominator, positioned below the line, defines the total number of equal parts into which the whole is divided. It establishes the context for the numerator, indicating the size of each individual part. In our example, 3⁄4, the denominator 4 signifies that the whole is divided into four equal parts.
Fraction Equivalence: Adjusting Numerators and Denominators
A fraction’s value can be expressed in various ways by adjusting the numerators and denominators. For instance, 6⁄8 can be simplified to 3⁄4 by dividing both the numerator and denominator by their greatest common divisor, which is 2. This process ensures that the fraction’s value remains the same while making it easier to work with.
Complex Fractions: Multiple Numerators and Denominators
In more complex fractions, there can be multiple numerators and denominators, especially when dealing with compound fractions or mixed numbers. For example, 5⁄6 + 7⁄8 could be considered as two fractions with multiple numerators and denominators. In such cases, simplifying and combining these fractions becomes essential for further calculations.
Visualizing Fractions: Using Diagrams and Models
Fractions can be visualized using diagrams and models, such as pie charts or number lines, to provide a clearer understanding of the relationship between the numerator and denominator. For instance, dividing a circle into four equal parts and shading three of them would visually represent the fraction 3⁄4.
Applying Fractions in Real-World Scenarios
Fractions are not merely theoretical concepts but are applied in various real-world situations. For instance, in cooking, recipes often involve fractions to measure ingredients accurately. In construction, fractions are used to determine proportions and measurements for structures. Understanding how to work with numerators and denominators is crucial for these practical applications.
Conclusion: Mastering Fraction Fundamentals
Grasping the fundamentals of numerators and denominators is the first step towards mastering fractions. By understanding their roles and relationships, individuals can effectively simplify, compare, and manipulate fractions. This knowledge forms the foundation for more advanced mathematical concepts and problem-solving skills.
Key Takeaway:
Understanding the relationship between numerators and denominators is essential for effective fraction manipulation, with real-world applications ranging from cooking to construction.
Can a numerator be a fraction itself?
+Yes, a numerator can indeed be a fraction. In such cases, the fraction is often called a “complex fraction.” For example, in the fraction 3⁄4, the numerator 3 is a whole number, but it could also be a fraction, such as 3⁄5. When working with complex fractions, it’s essential to simplify and manipulate them to make calculations easier.
What is the significance of the denominator in a fraction?
+The denominator defines the number of equal parts into which the whole is divided. It provides the context for the numerator, indicating the size of each individual part. For instance, in the fraction 3⁄4, the denominator 4 signifies that the whole is divided into four equal parts. Understanding the denominator is crucial for interpreting the fraction’s value.
How do I simplify fractions with large numerators and denominators?
+Simplifying fractions with large numerators and denominators involves finding the greatest common divisor (GCD) of both numbers. You can then divide both the numerator and denominator by the GCD to reduce the fraction to its simplest form. For example, to simplify 24⁄36, the GCD is 12, so you would divide both numbers by 12, resulting in the simplified fraction 2⁄3.
Are there any real-world examples where complex fractions are used?
+Yes, complex fractions are used in various real-world scenarios. For instance, in chemistry, fractions are used to represent the ratio of elements in a compound. In engineering, complex fractions might be used to calculate the strength of a material relative to its weight. Understanding complex fractions is essential for professionals in these fields.
How can I visually represent a fraction with a diagram?
+You can use visual aids like pie charts or number lines to represent fractions. For example, to represent 3⁄4, you could divide a circle into four equal parts and shade three of them. This visual representation provides a concrete understanding of the fraction’s value and its relationship to the whole.


