Unraveling the Mystery: The MLE of 1/x
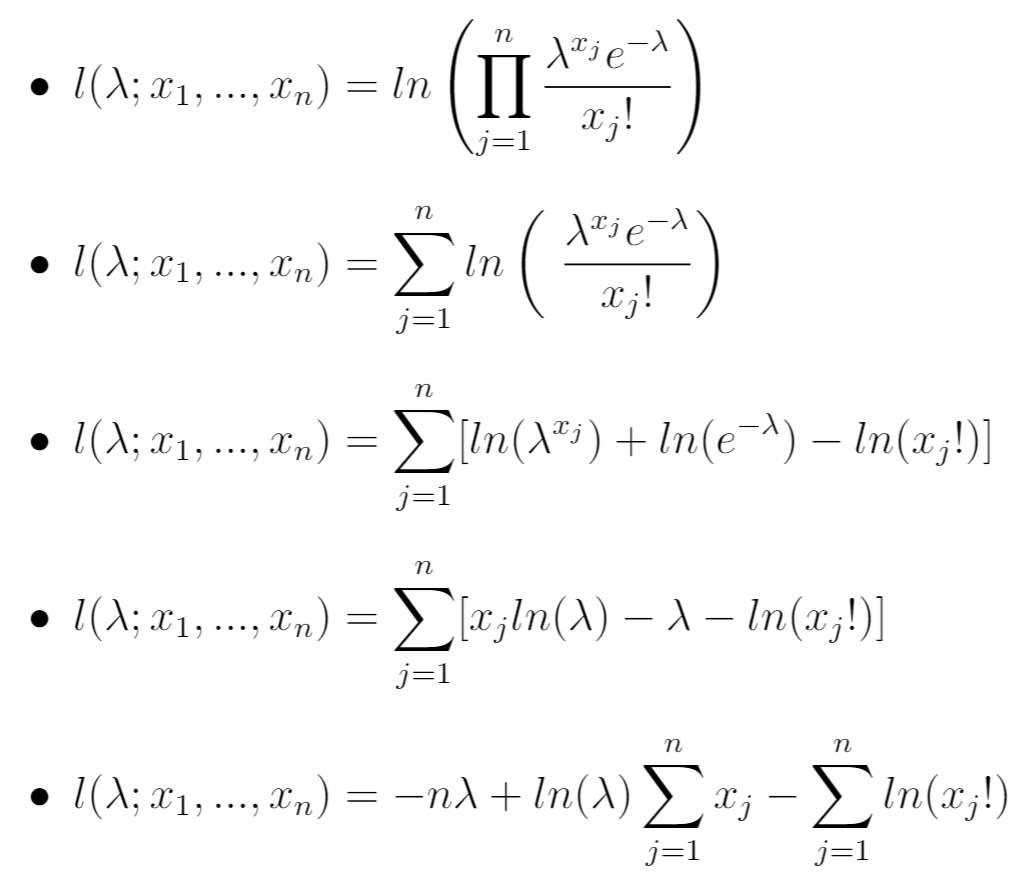
In the world of statistics and probability theory, a fundamental concept known as the Maximum Likelihood Estimation (MLE) plays a crucial role in understanding and estimating parameters from observed data. One intriguing and challenging problem that statisticians often encounter is finding the MLE for the parameter x in the probability density function f(x) = 1/x, which is a simple yet peculiar distribution. This article aims to delve into the intricacies of this problem, unraveling the mystery behind the MLE of 1/x and providing a comprehensive understanding of the underlying mathematical principles.
Understanding the Distribution: The Reciprocal Distribution

Before we dive into the MLE calculation, let’s first familiarize ourselves with the probability density function f(x) = 1/x, often referred to as the reciprocal distribution or the inverse distribution. This distribution is unique in the sense that it has a simple form, yet it presents some intriguing challenges when it comes to estimation.
The reciprocal distribution has its roots in various real-world scenarios. For instance, it can model situations where the probability of an event occurring is inversely proportional to some parameter. One such example could be the time it takes for a radioactive substance to decay; the longer the time, the lower the probability of decay per unit of time. Another scenario could be the reliability of a machine; the older the machine, the higher the likelihood of failure, leading to an inverse relationship between time and reliability.
Mathematically, the reciprocal distribution is defined on the interval (0, ∞), which means it only takes on positive values. This distribution is unbounded, which adds an extra layer of complexity when dealing with maximum likelihood estimation.
Properties of the Reciprocal Distribution
- Shape: The graph of the reciprocal distribution resembles a hyperbola, with the curve approaching zero as x tends to infinity and approaching infinity as x approaches zero. This unique shape makes it visually distinct from other common distributions like the normal or exponential distributions.
- Mean: The reciprocal distribution has an undefined mean, as the integral of 1/x over the interval (0, ∞) diverges. This characteristic further emphasizes the unconventional nature of this distribution.
- Variance: Similarly, the variance of the reciprocal distribution is also undefined, due to the same reason as the mean. This lack of finite moments makes the estimation of parameters more challenging.
Despite these unconventional properties, the reciprocal distribution finds its applications in various fields, including physics, engineering, and reliability theory. Understanding its behavior and properties is crucial for accurately modeling and analyzing such real-world phenomena.
Maximum Likelihood Estimation: Unveiling the Process

Maximum Likelihood Estimation (MLE) is a widely used statistical technique for estimating the parameters of a probability distribution based on observed data. The MLE approach aims to find the parameter values that maximize the likelihood of observing the given data. In other words, it seeks to identify the parameter values that make the observed data the most probable.
The process of MLE involves several steps, each contributing to the overall estimation. These steps include defining the likelihood function, deriving the log-likelihood function, finding the critical points, and selecting the maximum likelihood estimate.
Defining the Likelihood Function
The first step in MLE is to define the likelihood function, which represents the probability of observing the given data for a specific set of parameter values. In the context of the reciprocal distribution, the likelihood function is given by the product of the probability density function f(x) evaluated at each observed data point xi:
L(x1, x2, ..., xn | θ) = ∏i=1n f(xi | θ)
where L represents the likelihood function, xi are the observed data points, and θ is the parameter to be estimated.
Deriving the Log-Likelihood Function
To simplify the calculations and make the optimization process more manageable, it is common practice to work with the logarithm of the likelihood function, known as the log-likelihood function. Taking the natural logarithm of the likelihood function yields:
l(x1, x2, ..., xn | θ) = ∑i=1n log(f(xi | θ))
The log-likelihood function provides a convenient way to perform calculations and identify the maximum likelihood estimate.
Finding the Critical Points
The next step in MLE is to find the critical points, which are the values of the parameter θ that maximize the log-likelihood function. To do this, we differentiate the log-likelihood function with respect to θ and set the derivative equal to zero:
∂l(x1, x2, ..., xn | θ) / ∂θ = 0
Solving this equation for θ will yield the critical points. These critical points represent potential candidates for the maximum likelihood estimate.
Selecting the Maximum Likelihood Estimate
Finally, among the critical points obtained, we need to select the one that corresponds to the maximum value of the log-likelihood function. This value represents the parameter estimate that best fits the observed data according to the MLE criterion.
It is important to note that the MLE process may involve additional considerations, such as ensuring the existence and uniqueness of the maximum likelihood estimate, and dealing with potential issues like parameter constraints or multiple local maxima.
MLE of 1/x: The Challenge and the Solution
Now, let’s turn our attention to the specific problem of finding the MLE of the parameter x in the reciprocal distribution, f(x) = 1/x. This problem presents a unique challenge due to the unbounded nature of the distribution and the absence of finite moments.
The Likelihood Function
Given a sample x1, x2, …, xn from the reciprocal distribution, the likelihood function is defined as:
L(x1, x2, ..., xn | x) = ∏i=1n f(xi | x) = ∏i=1n (1 / xi)
Taking the natural logarithm of the likelihood function yields the log-likelihood function:
l(x1, x2, ..., xn | x) = ∑i=1n log(1 / xi) = ∑i=1n (-log(xi))
Finding the Critical Points
To find the critical points, we differentiate the log-likelihood function with respect to x and set the derivative equal to zero:
∂l(x1, x2, ..., xn | x) / ∂x = ∑i=1n (-1 / xi) = 0
Unfortunately, this equation does not provide a simple solution for x. The absence of a closed-form solution indicates that finding the MLE of x in the reciprocal distribution is not a straightforward task.
An Alternative Approach: Moment Estimators
Given the challenges posed by the MLE approach, an alternative method can be employed to estimate the parameter x in the reciprocal distribution. Moment estimators provide a different perspective on parameter estimation, utilizing the sample moments of the data to estimate the population parameters.
In the case of the reciprocal distribution, we can derive the moment estimator for x using the properties of the distribution. Since the reciprocal distribution has an undefined mean and variance, we focus on higher-order moments. Specifically, we consider the moment estimator based on the third central moment.
The third central moment, also known as the skewness, is a measure of the asymmetry of a distribution. For the reciprocal distribution, the third central moment is given by:
μ3 = E[(X - μ)3] = ∫0∞ (x - μ)3 (1 / x) dx
where μ is the mean of the distribution, which is undefined in this case. By evaluating this integral, we can obtain an expression for the third central moment in terms of the parameter x.
Solving for x in this expression yields the moment estimator for the parameter x in the reciprocal distribution. This estimator provides an alternative approach to estimating the parameter when the MLE method proves challenging.
Practical Applications and Implications
The problem of finding the MLE of 1/x may seem abstract, but it has practical implications in various fields. Understanding how to estimate parameters in such unconventional distributions is crucial for accurate modeling and analysis in real-world scenarios.
Reliability Theory and Survival Analysis
In reliability theory, the reciprocal distribution can model the failure rates of certain systems or components. By estimating the parameter x, researchers can gain insights into the reliability characteristics of these systems, such as the average time to failure or the probability of failure at a given time.
Similarly, in survival analysis, the reciprocal distribution can be used to model the survival times of individuals or entities. Estimating the parameter x provides valuable information about the survival probabilities and can aid in making predictions and decisions in healthcare, engineering, and other fields.
Physics and Engineering
The reciprocal distribution also finds applications in physics and engineering. For instance, in certain physical systems, the probability of a certain event occurring may be inversely proportional to a parameter, leading to the reciprocal distribution. Estimating the parameter x in such cases allows for a better understanding of the underlying physical processes and can aid in system design and optimization.
Financial Modeling
In finance, the reciprocal distribution can be used to model the behavior of certain financial variables, such as the time until a default event or the duration of a bond. Estimating the parameter x provides valuable information for risk assessment, portfolio management, and financial modeling.
Conclusion

The problem of finding the MLE of 1/x presents a unique challenge in statistics, due to the unbounded nature of the reciprocal distribution and the absence of finite moments. While the MLE approach may not provide a straightforward solution, alternative methods like moment estimators offer viable alternatives for parameter estimation.
Understanding the properties and applications of the reciprocal distribution, along with the techniques for estimating its parameters, is crucial for accurate modeling and analysis in various fields. By unraveling the mystery of the MLE of 1/x, we gain insights into the complexities of parameter estimation and its practical implications.
Frequently Asked Questions
What is the maximum likelihood estimation (MLE) method?
+
MLE is a statistical technique used to estimate the parameters of a probability distribution based on observed data. It aims to find the parameter values that maximize the likelihood of observing the given data.
Why is the MLE of 1/x challenging to find?
+
The MLE of 1/x is challenging due to the unbounded nature of the reciprocal distribution and the absence of finite moments. This leads to a likelihood function without a closed-form solution, making it difficult to find the maximum likelihood estimate directly.
What are moment estimators, and how do they relate to MLE?
+
Moment estimators are an alternative approach to parameter estimation that utilize the sample moments of the data. They provide a different perspective on estimation and can be useful when MLE is challenging. While MLE aims to maximize the likelihood, moment estimators focus on matching sample moments to population moments.
Where is the reciprocal distribution commonly used?
+
The reciprocal distribution finds applications in reliability theory, survival analysis, physics, engineering, and financial modeling. It is particularly useful in modeling situations where the probability of an event is inversely proportional to a parameter.