Unraveling the Mystery: 19/25 as a Percentage

Understanding Fractions as Percentages

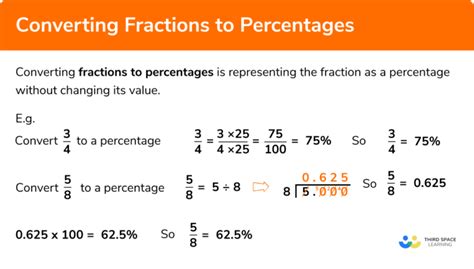
When we encounter fractions, it’s natural to want to express them in a more familiar format, such as percentages. Converting fractions to percentages helps us grasp the magnitude of the fraction in relation to the whole. Today, we’ll explore the process of transforming the fraction ¹⁹⁄₂₅ into a percentage, unraveling the mystery behind this mathematical concept.

The Fundamental Concept: Fractions and Percentages

At the core of our exploration, we must understand that fractions and percentages are interconnected representations of a part of a whole. A fraction, like ¹⁹⁄₂₅, signifies a division of a whole into 25 parts, and we have 19 of those parts. On the other hand, a percentage expresses the same concept as a fraction out of 100. So, when we convert ¹⁹⁄₂₅ to a percentage, we’re essentially finding the equivalent value in the context of a hundred parts.

Step-by-Step Conversion Process

1. Identify the Numerator and Denominator: Our fraction, ¹⁹⁄₂₅, has 19 as the numerator (the top number) and 25 as the denominator (the bottom number).

2. Convert the Fraction to a Decimal: To transform a fraction into a percentage, we first convert it into a decimal. This step is crucial as percentages are essentially decimals expressed as a fraction of 100. In this case, we divide 19 by 25: 19 ÷ 25 = 0.76.

3. Multiply by 100 to Find the Percentage: Now that we have the decimal representation, we multiply it by 100 to convert it into a percentage. This is a simple calculation: 0.76 × 100 = 76.

4. Express the Result as a Percentage: Finally, we express our result as a percentage. So, ¹⁹⁄₂₅ as a percentage is equal to 76%.

Visualizing the Conversion

To enhance our understanding, let’s visualize this conversion process. Imagine a whole divided into 25 equal parts. If we were to shade 19 of those parts, we’d have ¹⁹⁄₂₅ of the whole shaded. Now, consider that each part represents 4% of the whole (since there are 25 parts in total). So, 19 parts shaded would equate to 19 × 4% = 76%.

Real-World Applications

Converting fractions to percentages has numerous real-world applications. For instance, in finance, percentages are often used to express interest rates or returns on investments. In cooking, recipes might provide ingredient quantities as fractions, but we may need to convert them to percentages to ensure accurate measurements. Understanding this conversion process empowers us to make sense of data presented in various forms.

A Look at Other Fractions

While we’ve focused on ¹⁹⁄₂₅, it’s worth noting that this conversion method applies to all fractions. Whether it’s ³⁄₈, ⁵⁄₁₂, or any other fraction, the steps remain the same. The beauty of mathematics lies in its consistency and predictability.

Key Takeaway:

Converting fractions to percentages is a fundamental skill that allows us to interpret data in a more intuitive manner. By understanding the underlying concept and following a systematic process, we can effortlessly convert fractions like ¹⁹⁄₂₅ into a percentage representation, providing a clearer understanding of the fraction’s value.

FAQ Section

    <div class="faq-item">
        <div class="faq-question">
            <h3>Can all fractions be converted to percentages, or are there limitations to this conversion method?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Yes, all fractions can be converted to percentages using the method described. There are no inherent limitations to this conversion. However, it's important to note that the accuracy of the resulting percentage depends on the denominator of the fraction. For example, fractions with larger denominators might yield percentages with more decimal places.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>Why do we use percentages instead of just keeping fractions? What are the advantages of converting to percentages?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Percentages provide a standardized way of expressing parts of a whole, making it easier to compare values. They are widely used in various fields, such as finance, statistics, and everyday life. Converting fractions to percentages helps us make sense of data in a more intuitive and familiar way, allowing for better understanding and communication of quantitative information.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>Are there any shortcuts or tricks to convert fractions with larger denominators, like 13/45, to percentages more efficiently?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>While there are no universal shortcuts for all fractions, you can simplify the fraction before converting it to a percentage. For instance, in the case of 13/45, you can simplify it to 13/45 = 1/3 + 2/15. This way, you only need to convert 1/3 and 2/15 separately and then add the resulting percentages. However, for complex fractions, it's often more straightforward to follow the standard conversion process.</p>
        </div>
    </div>
</div>