Calculate Hemisphere Volume: 5 Simple Steps
Understanding Hemisphere Volume
Calculating the volume of a hemisphere involves a straightforward process that leverages fundamental geometric principles. This calculation is particularly useful in various fields, from architecture and engineering to physics and astronomy, where understanding the three-dimensional space occupied by hemispherical objects is essential. Here, we’ll guide you through a five-step process to determine the volume of a hemisphere, a crucial skill for anyone working with these unique shapes.
Step 1: Define the Hemisphere’s Radius
The radius of a hemisphere is a critical parameter in determining its volume. This radius is the distance from the center of the hemisphere to its outer surface. It is often denoted as ‘r’ in mathematical equations and is measured in units such as meters, feet, or centimeters, depending on the context of the problem.
Step 2: Understand the Formula
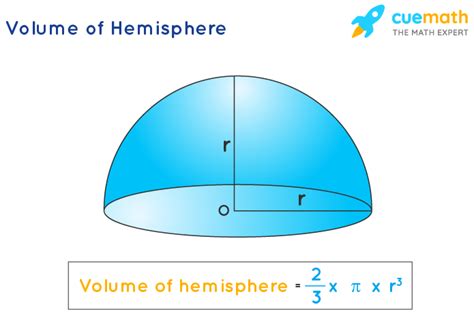
The formula for calculating the volume of a hemisphere is a straightforward extension of the formula for the volume of a sphere. For a hemisphere, the volume (V) is given by the formula:
\[ \begin{equation*} V = \frac{2}{3} \pi r^3 \end{equation*} \]
where \pi (pi) is a mathematical constant approximately equal to 3.14159, and r is the radius of the hemisphere. This formula represents the volume of the three-dimensional space occupied by the hemisphere.
Step 3: Plug in the Radius Value
Once you have the radius of the hemisphere, simply plug it into the formula. Ensure that the units of the radius are consistent with the desired units for the volume. For instance, if the radius is given in centimeters, the volume will also be in cubic centimeters.
Step 4: Calculate the Volume
With the formula and the radius value in hand, the next step is to perform the calculation. Using a calculator, or even by hand, compute the value of 2/3 \pi r^3. This will give you the volume of the hemisphere.
Step 5: Interpret the Result
The calculated volume represents the amount of space occupied by the hemisphere. This value can be used in various practical applications, such as determining the capacity of a hemispherical container, designing structures with hemispherical elements, or even in astronomical calculations involving celestial bodies.
A Real-World Example
Let’s consider a practical scenario: a landscape architect is designing a hemispherical water feature for a park. The radius of the hemisphere is 2 meters. Using the formula, the volume of the water feature can be calculated as:
\[ \begin{align*} V &= \frac{2}{3} \pi (2 \text{ m})^3 \\ &= \frac{2}{3} \pi (8 \text{ m}^3) \\ &\approx 17.04 \text{ m}^3 \end{align*} \]
So, the volume of the water feature is approximately 17.04 cubic meters. This value helps the architect determine the amount of water required to fill the feature and ensures the design meets the intended visual and functional requirements.
Conclusion
Calculating the volume of a hemisphere is a fundamental skill with wide-ranging applications. By following these five simple steps, anyone can determine the volume of a hemisphere with ease. This calculation highlights the beauty of mathematics and its ability to describe and quantify the world around us.



