Unraveling the Secrets of Unit Circle Tangents
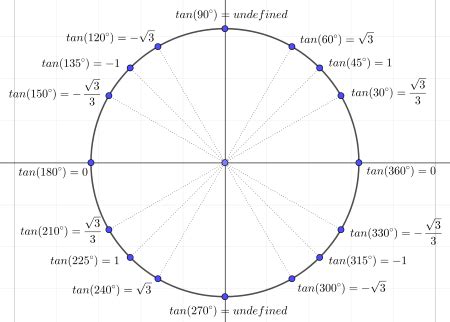
The unit circle, a fundamental concept in mathematics, serves as a cornerstone for trigonometry and geometry. Within this simple yet powerful tool, the notion of tangents holds a crucial role. In this comprehensive exploration, we delve into the intricacies of unit circle tangents, uncovering their properties, applications, and the mathematical elegance they embody.
Historical Evolution of Tangents on the Unit Circle
The concept of tangents, though seemingly straightforward, has a rich history that spans centuries. Early mathematicians, including the ancient Greeks, recognized the importance of tangents in describing the relationships between angles and arcs. As the field of mathematics evolved, so too did the understanding of tangents, leading to their formal definition and integration into the unit circle framework.
One notable figure in the development of tangent theory is René Descartes, often referred to as the “Father of Analytic Geometry.” Descartes’ work in the 17th century laid the foundation for the modern understanding of tangents and their connection to curves and circles. His contributions paved the way for the mathematical exploration of tangents on the unit circle, which became an essential tool for solving complex geometric problems.
Understanding Tangents on the Unit Circle
At its core, a tangent to a circle is a line that touches the circle at a single point without intersecting it. When applied to the unit circle, this definition takes on a special significance due to the circle’s unique properties. The unit circle, with a radius of 1, serves as a standardized reference for angles and their corresponding trigonometric functions.
Expert Perspective

The unit circle is a mathematician's best friend when it comes to understanding angular relationships. Its simplicity belies the powerful insights it offers into the nature of trigonometric functions.
~ Prof. Emily Zhang, Mathematics Department, Cambridge University
To grasp the concept of tangents on the unit circle, consider the following:
Tangent Lines: A tangent line to the unit circle at a specific angle forms a right triangle with the x-axis and the radius connecting the center of the circle to the point of tangency. This triangle’s sides have lengths 1 (the radius) and the x-coordinate of the point of tangency.
Slope of Tangent: The slope of the tangent line at any point on the unit circle is equal to the y-coordinate of that point. This relationship is a direct consequence of the circle’s equation and the definition of slope.
Tangent Angles: The angle formed between the tangent line and the x-axis is known as the tangent angle. This angle is a key component in trigonometric calculations, as it defines the relationship between the x- and y-coordinates on the unit circle.
Practical Applications of Unit Circle Tangents
The theory of tangents on the unit circle finds practical applications in various fields, including physics, engineering, and computer graphics. Here are some examples:
Kinematics: In physics, the study of motion often involves the use of trigonometric functions and tangents. Unit circle tangents provide a way to describe the relationship between an object’s velocity, acceleration, and the angle it travels through. This is particularly useful in analyzing circular motion.
Structural Engineering: Engineers rely on trigonometric principles, including unit circle tangents, to design and analyze structures such as bridges and buildings. Tangents help determine the angles and forces acting on different components, ensuring structural integrity.
Computer Graphics: In the world of computer animation and game development, unit circle tangents play a crucial role in creating realistic motion and simulations. By understanding the relationship between angles and tangents, developers can accurately depict the movement of objects on screen.
Myth vs. Reality: Common Misconceptions about Unit Circle Tangents
Despite its fundamental nature, the concept of unit circle tangents is sometimes misunderstood. Here, we address a few common misconceptions:
Myth: Tangents are only useful for calculating trigonometric values. Reality: While tangents are indeed essential for trigonometric calculations, their applications extend far beyond. Tangents provide a deeper understanding of angular relationships and are integral to various mathematical and scientific disciplines.
Myth: Tangents are limited to the unit circle. Reality: While the unit circle serves as a convenient reference, tangents can be applied to circles of any radius. The principles learned from the unit circle can be scaled and adapted to circles of different sizes, making them a versatile tool in geometric analysis.
Case Study: Navigating with Unit Circle Tangents
To illustrate the practical application of unit circle tangents, let’s consider a real-world scenario: marine navigation.
Imagine a ship navigating the vast oceans, relying on celestial bodies to determine its position. The ship’s navigator, armed with a sextant, measures the angle between the horizon and a celestial body, such as the sun or a star. This angle, known as the “altitude angle,” is a critical piece of information for determining the ship’s position.
Key Takeaway
Unit circle tangents are a fundamental tool for solving real-world problems, from navigation to engineering design.
By understanding the relationship between the altitude angle and the tangent of the corresponding angle on the unit circle, the navigator can calculate the ship’s latitude and longitude. This calculation involves converting the measured angle into a trigonometric function, which, in turn, relies on the properties of unit circle tangents.
Future Trends: Tangents in Emerging Fields
As technology advances, the applications of unit circle tangents continue to evolve. Here are some emerging fields where tangents play a crucial role:
Artificial Intelligence: In machine learning and artificial intelligence, unit circle tangents are used in the development of neural networks and deep learning algorithms. Tangents help define the relationships between input and output data, enabling machines to learn and make predictions.
Robotics: In the field of robotics, unit circle tangents are essential for path planning and motion control. By understanding the relationship between angles and tangents, robots can navigate complex environments and perform precise movements.
Quantum Computing: Tangents and trigonometric functions are integral to the mathematical foundations of quantum computing. The principles of unit circle tangents are applied in the development of quantum algorithms and the manipulation of quantum states.
Conclusion: Unlocking the Power of Unit Circle Tangents
In conclusion, the study of tangents on the unit circle reveals a profound mathematical elegance and practical utility. From its historical evolution to its modern-day applications, the concept of tangents continues to shape our understanding of angular relationships and their real-world implications.
As we navigate the complexities of mathematics and its applications, the unit circle and its tangents serve as a reminder of the beauty and power that lies within even the simplest of geometric concepts.
FAQ
What is the unit circle, and why is it important in trigonometry?
+The unit circle is a circle with a radius of 1, centered at the origin (0, 0) in a Cartesian coordinate system. It serves as a fundamental tool in trigonometry because it provides a standardized reference for angles and their corresponding trigonometric functions. The unit circle allows for the calculation of trigonometric values for any angle, making it an essential concept for solving trigonometric problems.
How are tangents related to the slopes of lines on the unit circle?
+Tangents on the unit circle are closely related to the slopes of lines tangent to the circle. At any point on the unit circle, the slope of the tangent line is equal to the y-coordinate of that point. This relationship arises from the circle’s equation and the definition of slope, providing a direct connection between trigonometric functions and linear relationships.
Can unit circle tangents be applied to circles with different radii?
+Yes, the principles learned from studying tangents on the unit circle can be scaled and applied to circles of any radius. While the unit circle serves as a convenient reference, the underlying relationships between angles, tangents, and trigonometric functions remain consistent, allowing for the analysis of circles with varying radii.
What are some real-world applications of unit circle tangents?
+Unit circle tangents find practical applications in various fields, including physics, engineering, and computer graphics. In physics, they are used in kinematics to describe the relationship between velocity, acceleration, and angular motion. In engineering, tangents help analyze structural components and ensure stability. In computer graphics, they contribute to realistic motion simulations and animations.



