The Secrets of Sin and Cos on the Unit Circle
The unit circle, a simple geometric concept, holds within it a treasure trove of mathematical secrets, particularly when it comes to the functions sin (sine) and cos (cosine). These functions, fundamental to trigonometry, are not just theoretical constructs but practical tools with real-world applications. Let’s delve into the depths of the unit circle to uncover the mysteries of sin and cos and understand why they are so crucial in the realm of mathematics.
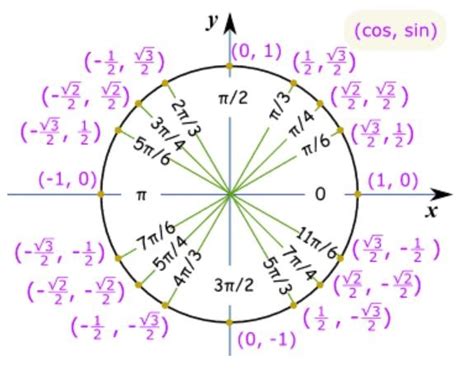
The unit circle, a circle with a radius of 1 centered at the origin (0,0) on a Cartesian plane, is a basic yet powerful tool. It serves as a bridge between geometry and trigonometry, providing a visual representation of angles and their corresponding trigonometric values. When we place an angle on the unit circle, we can easily find the coordinates of the point where the angle’s terminal side intersects the circle. These coordinates are none other than the values of cosine and sine for that particular angle.
Imagine the unit circle as a magical compass, where every angle reveals a unique story through its corresponding sine and cosine values. These values are not just numbers but mathematical ambassadors, carrying messages about the angle's position and orientation within the circle.
The Basics: Sine and Cosine

Sine and cosine are trigonometric functions that relate the angles of a right triangle to the ratios of its sides. In the context of the unit circle, these functions take on a more visual and intuitive meaning. Let’s break it down:
Sine (sin): When we place an angle θ on the unit circle, the y-coordinate of the point where the terminal side intersects the circle is the sine value of that angle. In other words, sin(θ) represents the height of the point above or below the x-axis. It tells us how far we are vertically from the center of the circle.
Cosine (cos): Similarly, the x-coordinate of the same point on the unit circle is the cosine value of the angle. So, cos(θ) represents the distance we are horizontally from the y-axis. It measures the position of the point along the x-axis.
Pros of Understanding Sine and Cosine on the Unit Circle
- Visual intuition: The unit circle provides a clear, visual representation of the relationships between angles and trigonometric functions.
- Simplicity: With a radius of 1, all angles and their corresponding trigonometric values are easily relatable.
- Consistency: The unit circle ensures that trigonometric functions are standardized and consistent across different angles.
Cons and Limitations
- Angle restrictions: The unit circle is limited to angles between 0 and 360 degrees (or 0 and 2π radians), which may not cover all real-world scenarios.
- Complex numbers: For angles outside the unit circle's range, trigonometric functions involve complex numbers, adding a layer of complexity.
The Power of Trigonometric Functions

Sine and cosine are not mere mathematical curiosities; they are powerful tools with a wide range of applications:
Physics and Engineering: In physics, trigonometric functions describe the motion of objects, the behavior of waves, and the relationships between forces. For example, the sine function is used to model simple harmonic motion, like the motion of a mass on a spring.
Electrical Engineering: In electrical circuits, sine waves are used to represent alternating current (AC) signals, which are essential for understanding power transmission and signal processing.
Astronomy and Navigation: Trigonometric functions are crucial for calculating the positions of celestial bodies and navigating on Earth. They are used in celestial mechanics to predict the motion of planets and in navigation systems to determine positions and directions.
Computer Graphics: In computer graphics and animation, trigonometric functions are used to create realistic 3D models, animate objects, and simulate physical phenomena like light and shadow.
Historical Perspective
The study of trigonometry, and thus the understanding of sine and cosine, has a rich historical background. Ancient civilizations, including the Greeks and Indians, made significant contributions to trigonometry. However, it was the Arab mathematician Muhammad ibn Jābir al-Ḥarrānī al-Battānī, known as Albategnius, who first introduced the concept of the unit circle to trigonometry in the 9th century.
Real-World Applications
Let’s explore a practical example of how sine and cosine functions are used in real-world scenarios:
Scenario: Imagine you are an engineer designing a bridge across a river. You need to calculate the height of the bridge pillars to ensure they can support the weight of the bridge and withstand the forces of nature.
Solution: Using trigonometric functions, you can model the forces acting on the bridge pillars. The sine function can help you calculate the vertical component of the force due to wind or water currents, while the cosine function can determine the horizontal component of the force. By accurately modeling these forces, you can design a safe and stable bridge.
Visualizing Trigonometric Functions

To truly grasp the power of sine and cosine, let’s visualize their behavior on the unit circle:
As we move around the unit circle, the values of sine and cosine oscillate between -1 and 1, creating a wave-like pattern. This wave pattern is a fundamental characteristic of trigonometric functions and is used to model periodic phenomena in various fields.
Advanced Topics
For those eager to explore further, the study of sine and cosine on the unit circle opens up several advanced mathematical concepts:
Taylor Series: The Taylor series expansion of sine and cosine functions provides an analytical representation of these functions as an infinite series of polynomials.
Complex Analysis: Trigonometric functions play a crucial role in complex analysis, where they are used to analyze functions of complex variables and solve complex equations.
Fourier Series: In signal processing, the Fourier series decomposes periodic functions into a sum of sine and cosine waves, allowing for the analysis and manipulation of signals.
Conclusion
The unit circle, with its sine and cosine functions, is a powerful tool that bridges the gap between geometry and trigonometry. It provides a visual and intuitive understanding of angles and their trigonometric values. From physics to engineering and computer graphics, the applications of sine and cosine are vast and diverse. By exploring these functions, we unlock a world of mathematical secrets and gain a deeper appreciation for the beauty and utility of trigonometry.
How do sine and cosine values change as we move around the unit circle?
+As we move counterclockwise around the unit circle, the sine values follow a wave-like pattern, oscillating between -1 and 1. Meanwhile, the cosine values also oscillate but are shifted by π/2 radians (90 degrees). This shift creates a complementary relationship between sine and cosine.
What happens when we use angles outside the unit circle’s range?
+When we use angles greater than 360 degrees (or 2π radians), we enter the realm of complex numbers. Trigonometric functions for these angles involve complex values, adding a layer of complexity to the calculations.
Can sine and cosine be used to model non-periodic phenomena?
+While sine and cosine are excellent for modeling periodic phenomena, they are less effective for non-periodic events. In such cases, other mathematical functions, such as exponential or logarithmic functions, may be more suitable.
Are there any practical limitations to using the unit circle for trigonometry?
+Yes, the unit circle has a limited range of angles, which may not cover all real-world scenarios. For angles outside this range, more advanced mathematical techniques, such as the use of inverse trigonometric functions or trigonometric identities, are required.



