Unveiling the Secrets of Trig Inverse Derivatives

The world of calculus is a fascinating one, filled with intricate concepts and mathematical mysteries. Among these, the derivatives of inverse trigonometric functions, often referred to as inverse trig derivatives, hold a special place. These derivatives are not merely theoretical constructs but powerful tools with practical applications in various fields. Understanding them can unlock a deeper comprehension of calculus and its real-world implications. In this article, we embark on a journey to explore the intricacies of inverse trig derivatives, delving into their definitions, formulas, and applications. So, let’s dive into the secrets of this mathematical realm and uncover the knowledge that lies within.

Understanding Inverse Trigonometric Functions

Before we delve into the derivatives, let’s refresh our understanding of inverse trigonometric functions. These functions are the inverses of the basic trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent. They are denoted as arcsin, arccos, arctan, arccsc, arcsec, and arccot, respectively. The key idea is that these inverse functions allow us to find the angle whose trigonometric value is a given number.

For instance, if we have the value of sin(x) = 0.5, we can use the arcsin function to find the angle x that corresponds to this value. This inverse relationship is a fundamental concept in trigonometry and forms the basis for many mathematical and scientific calculations.

Exploring the Derivatives

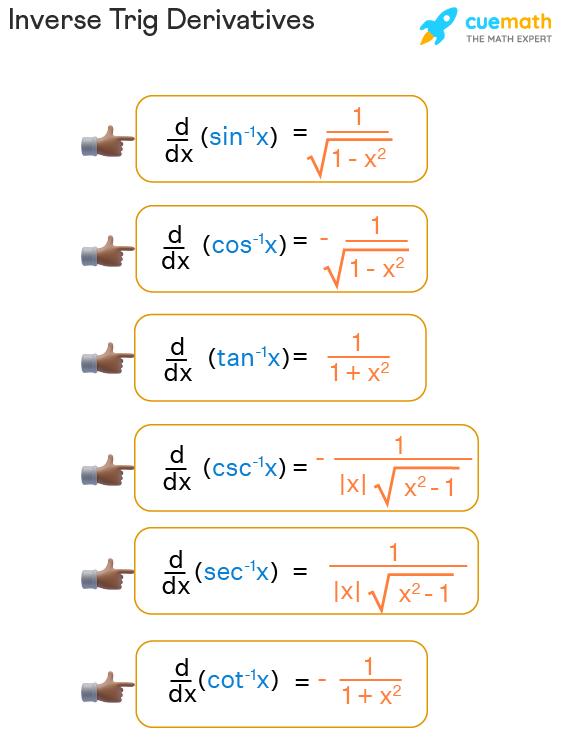
Now, let’s turn our attention to the derivatives of these inverse trigonometric functions. The derivative of a function, as we know, represents the rate of change of that function at a given point. In the context of inverse trig derivatives, we’re interested in how these functions change with respect to their arguments. Here’s a breakdown of the derivatives for each inverse trigonometric function:

Arcsin Derivative

The derivative of arcsin(x) is given by:

\[ \begin{equation*} \frac{d}{dx} (\arcsin(x)) = \frac{1}{\sqrt{1 - x^2}} \,. \end{equation*} \]

This derivative tells us how the arcsin function changes as we move along the x-axis. It’s essential to note that the derivative is undefined when x = 1 or x = -1, as these values are outside the defined range of arcsin(x).

Arccos Derivative

The derivative of arccos(x) is:

\[ \begin{equation*} \frac{d}{dx} (\arccos(x)) = -\frac{1}{\sqrt{1 - x^2}} \,. \end{equation*} \]

The negative sign in this derivative is a critical distinction from the arcsin derivative. It indicates that the arccos function changes in the opposite direction as we move along the x-axis.

Arctan Derivative

For arctan(x), the derivative is:

\[ \begin{equation*} \frac{d}{dx} (\arctan(x)) = \frac{1}{1 + x^2} \,. \end{equation*} \]

This derivative is always positive, indicating that the arctan function consistently increases as we move along the x-axis.

Arccsc, Arcsec, and Arccot Derivatives

The derivatives for the remaining inverse trigonometric functions, arccsc(x), arcsec(x), and arccot(x), can be derived using similar principles. These derivatives are more complex and involve the absolute value function, but they provide valuable insights into how these functions behave.

Applications in Real-World Scenarios

Inverse trig derivatives have a wide range of applications in various fields, including physics, engineering, and computer science. Here are a few examples to illustrate their practical significance:

Physics and Mechanics

In physics, inverse trig derivatives are used to analyze the motion of objects. For instance, when calculating the angle of elevation or depression of an object, the arctan derivative can be employed. This is particularly useful in scenarios involving projectile motion or inclined planes.

Additionally, in mechanics, inverse trig derivatives are crucial for understanding the behavior of springs and pendulums. The arccos derivative, for example, can help determine the angle at which a spring reaches its maximum compression or extension.

Engineering and Design

Engineers often rely on inverse trig derivatives to design structures and systems. For instance, when designing a bridge or a tower, the arcsin derivative can be used to calculate the angle of inclination, ensuring stability and structural integrity.

Furthermore, in electrical engineering, inverse trig derivatives are used to analyze the behavior of circuits, particularly in the context of AC signals and phase angles.

Computer Graphics and Animation

In the world of computer graphics and animation, inverse trig derivatives play a vital role in creating realistic motion. For example, when animating a character walking up a slope, the arctan derivative can be used to determine the angle of inclination, resulting in smooth and natural movement.

Advanced Topics and Extensions

The study of inverse trig derivatives opens up a realm of advanced mathematical concepts. Here are a few extensions and topics worth exploring:

Composite Functions and Chain Rule

When dealing with composite functions involving inverse trigonometric functions, the chain rule becomes essential. The chain rule allows us to find the derivative of a composite function by considering the derivatives of its individual components. This is particularly useful when working with functions like sin(arcsin(x)) or cos(arccos(x)).

Higher-Order Derivatives

Beyond the first derivative, we can explore higher-order derivatives of inverse trigonometric functions. These derivatives provide insights into the rate of change of the rate of change, offering a deeper understanding of the function’s behavior. For instance, the second derivative of arcsin(x) can reveal interesting patterns and characteristics.

Integration Techniques

Inverse trig derivatives are not only relevant in differentiation but also in integration. The knowledge of these derivatives can assist in finding integrals of trigonometric functions. Techniques like integration by parts and trigonometric substitutions often involve inverse trig derivatives.

Conclusion: Unlocking Mathematical Mastery

In the realm of calculus, inverse trig derivatives are like hidden gems, waiting to be discovered and utilized. By understanding these derivatives, we gain a deeper appreciation for the beauty and practicality of mathematics. They provide us with the tools to solve complex problems and explore the wonders of the natural world.

As we conclude our journey through the secrets of inverse trig derivatives, we hope you’ve gained valuable insights and a renewed enthusiasm for mathematics. Remember, every mathematical concept, no matter how complex, has its unique applications and contributions to our understanding of the universe.

FAQ