3 Tips on Equality Transitivity

The concept of equality transitivity is a fundamental principle in mathematics and logic, but it extends far beyond the realm of equations and symbols. In our daily lives, understanding and applying this principle can lead to fairer decisions, more accurate conclusions, and a better grasp of the world around us. Here, we delve into three practical tips to help navigate the often complex world of equality transitivity.
1. Recognizing Equality: A Universal Language
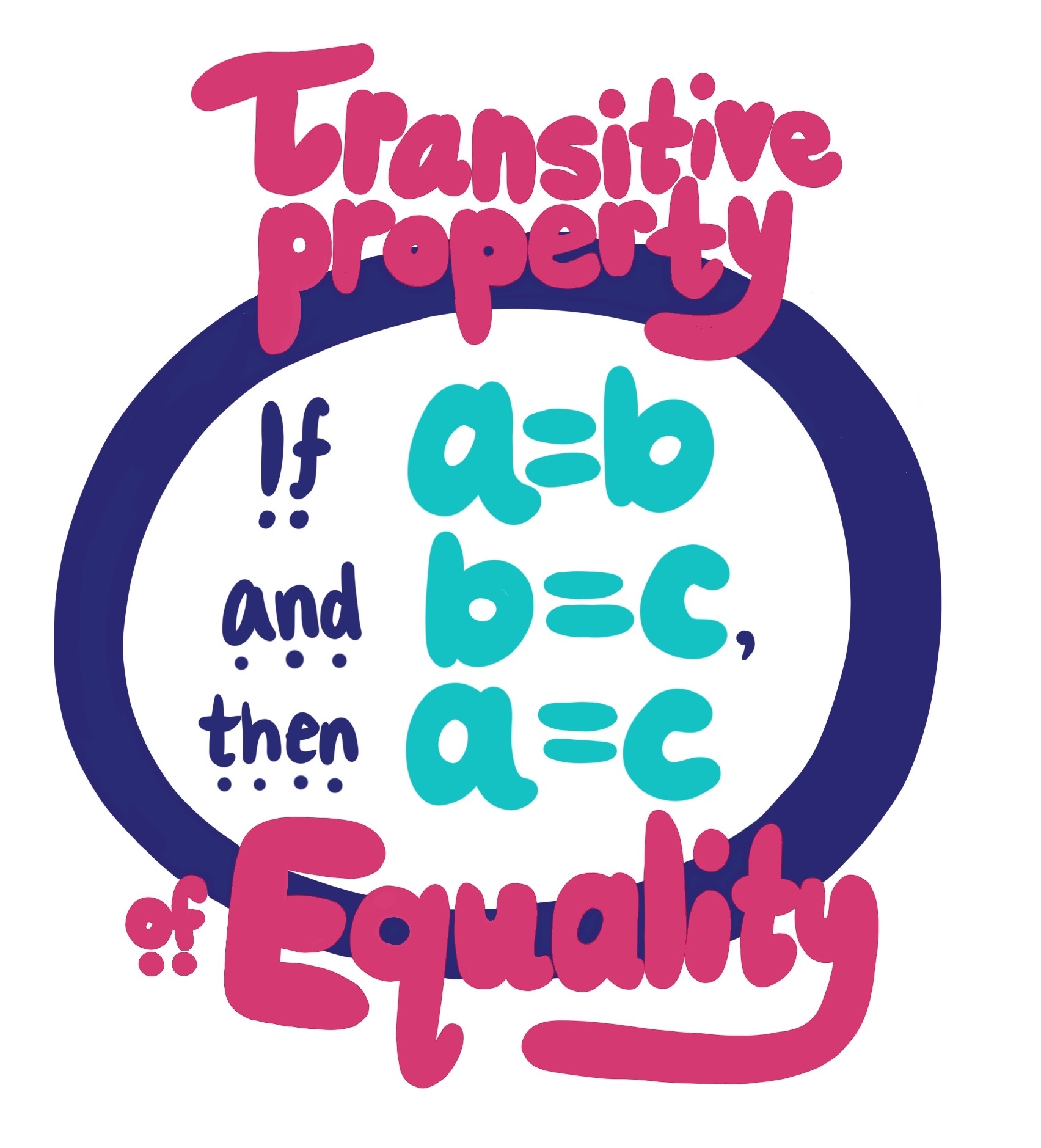
Equality, at its core, is a universal concept. It transcends cultural, linguistic, and societal boundaries. When we say ‘A is equal to B,’ we are not just using a mathematical term; we are expressing a fundamental truth about the nature of things. Recognizing equality in various forms and contexts is the first step towards mastering equality transitivity.
Consider the following scenario: you are shopping for apples. You pick up two apples that look identical in size, color, and texture. Your initial assessment is that these apples are equal in value and quality. However, upon weighing them, you find that one apple is slightly heavier. Despite this difference, you can still confidently state that these apples are equal in a broader sense. They are equal in their essence as apples, their contribution to a pie, or their ability to satisfy your hunger.
2. Transitivity: A Tool for Logical Consistency

The transitivity of equality is a powerful tool for maintaining logical consistency. It ensures that if A is equal to B, and B is equal to C, then A must also be equal to C. This principle is not limited to mathematical equations; it applies to a wide range of scenarios.
Take, for instance, the process of hiring for a job. If you have two equally qualified candidates, Candidate A and Candidate B, and you decide that Candidate A is the better fit, then your decision should be consistent if Candidate B and Candidate C are also equally qualified. If you decide that Candidate B is better than Candidate C, and Candidate C is better than Candidate A, you have a logical inconsistency. This is where the transitivity of equality comes into play, helping you make fair and consistent decisions.
3. Beyond Mathematics: Equality Transitivity in Everyday Life
While equality transitivity is a mathematical concept, its applications are far-reaching. It can guide us in making fair decisions, evaluating arguments, and solving real-world problems.
Let’s look at a social scenario. Imagine you are organizing a community event and you want to ensure equal participation from all members. You start by inviting a group of friends, all of whom are eager to attend. Then, you invite another group, and a third, and so on. If you treat each group equally, offering the same opportunities and information, you are applying the principle of equality transitivity. This ensures that your event is fair and inclusive, reflecting the principle that ‘all are equal’ in your community.
In conclusion, understanding and applying the concept of equality transitivity is a powerful skill. It helps us navigate the complexities of decision-making, argumentation, and problem-solving. By recognizing equality in its various forms and applying the principle of transitivity, we can make more logical and fair choices in our daily lives.
Equality transitivity is a tool for fairness and logical consistency, applicable across a wide range of situations.
What is the mathematical definition of equality transitivity?
+In mathematics, equality transitivity is a principle that states if A = B and B = C, then A = C. It ensures logical consistency in equations and expressions.
How does equality transitivity apply to real-world situations?
+Equality transitivity helps in making fair decisions, evaluating arguments, and ensuring consistency in various contexts, such as hiring processes or community event planning.
Can you provide an example of equality transitivity in everyday life?
+Consider a scenario where you are baking a cake and need to ensure equal portions for all guests. You first divide the cake into two equal halves, then divide each half into two equal quarters. Here, equality transitivity ensures that all portions are of the same size.
What are some common mistakes people make when applying equality transitivity?
+One common mistake is assuming that if A is equal to B and B is greater than C, then A must be greater than C. This is a violation of equality transitivity, as it ignores the fundamental principle of equality.


