How to Calculate a Pyramid's Surface Area
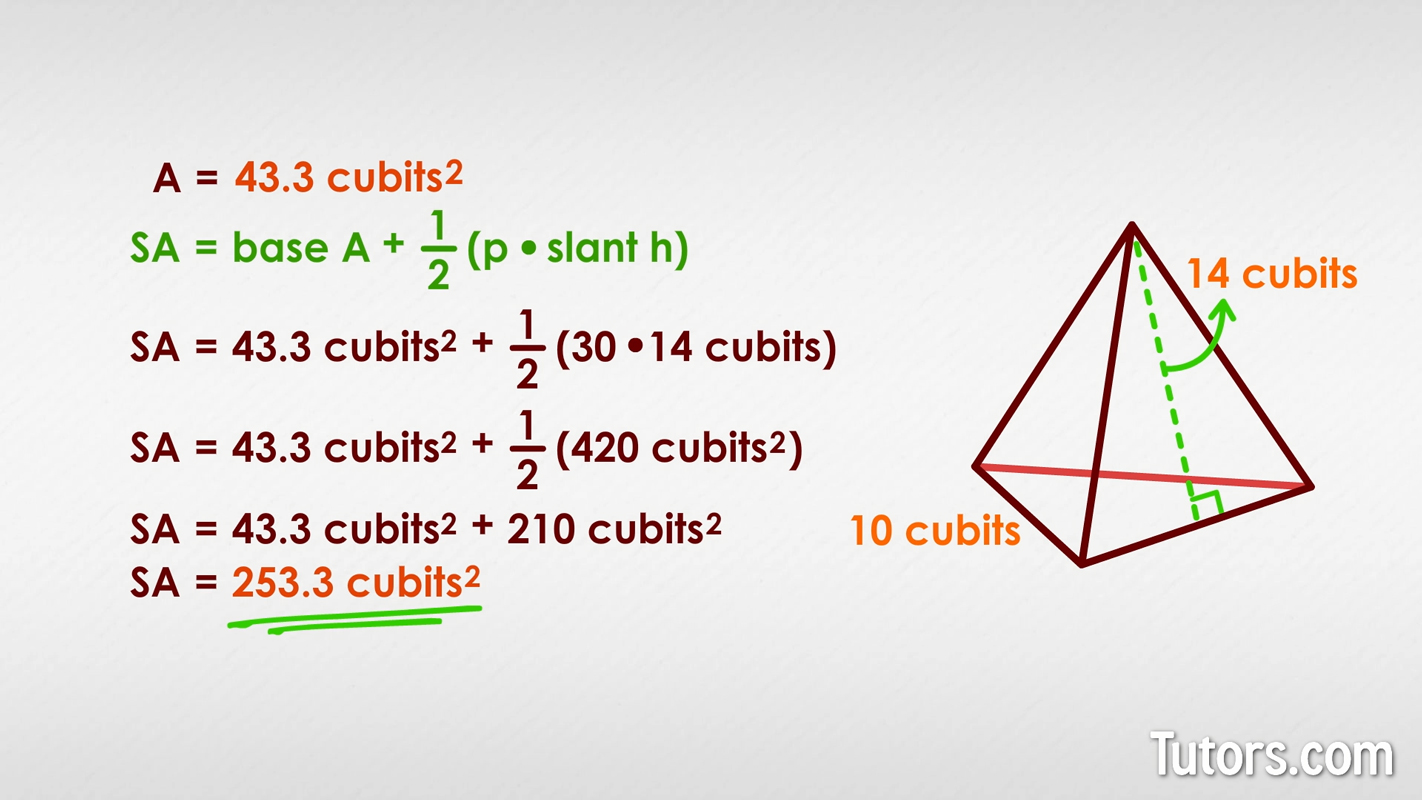
Calculating the surface area of a pyramid can be a fascinating journey into the world of geometry and spatial reasoning. Pyramids, with their unique and ancient architectural design, have captured the curiosity of mathematicians and engineers for centuries. Let’s embark on a step-by-step exploration to uncover the secrets behind determining a pyramid’s surface area.
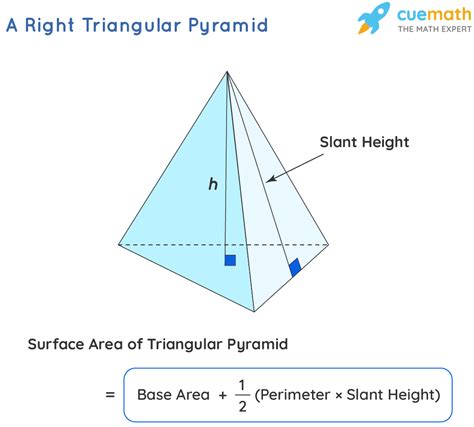
To begin, we must first grasp the fundamental components that make up a pyramid. At its core, a pyramid consists of a base and a set of triangular faces. The base can take various shapes, such as a square, triangle, or even a polygon, depending on the pyramid’s design. Each triangular face connects one corner of the base to the pyramid’s apex, creating a unique three-dimensional structure.
Now, let’s delve into the mathematical process of calculating the surface area. This calculation primarily involves two distinct parts: determining the area of the base and computing the areas of the triangular faces. By combining these two components, we can arrive at the total surface area of the pyramid.
Base Area Calculation
The base of a pyramid plays a pivotal role in determining its overall surface area. The shape and size of the base significantly influence the pyramid’s structural integrity and stability. To calculate the base area, we must consider the specific shape of the base.
For instance, if the base is a square, we can utilize the simple formula:
\[ \begin{equation*} \text{Base Area} = \text{side length} \times \text{side length} \, . \end{equation*} \]
However, if the base is a triangle, we need to employ the formula for the area of a triangle:
\[ \begin{equation*} \text{Base Area} = \frac{1}{2} \times \text{base length} \times \text{height} \, . \end{equation*} \]
By accurately measuring the dimensions of the base, we can determine its area and establish a foundation for further calculations.
Triangular Face Area Calculation
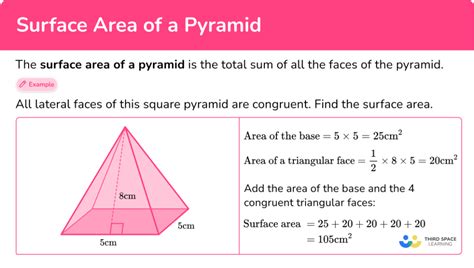
Each triangular face of a pyramid contributes to its overall surface area. These triangular faces, formed by connecting the corners of the base to the apex, create the pyramid’s iconic shape. To calculate the area of a triangular face, we can use the formula:
\[ \begin{equation*} \text{Triangular Face Area} = \frac{1}{2} \times \text{base of triangle} \times \text{height of triangle} \, . \end{equation*} \]
By measuring the base and height of each triangular face, we can determine its area. It’s important to note that the base of the triangular face refers to the side of the triangle that is not connected to the apex, while the height is the perpendicular distance from the base to the apex.
Total Surface Area Calculation
Once we have determined the areas of the base and each triangular face, we can proceed to calculate the total surface area of the pyramid. This calculation involves summing up the areas of all the faces, including the base.
The formula for the total surface area of a pyramid is as follows:
\[ \begin{equation*} \text{Total Surface Area} = \text{Base Area} + \text{Sum of Areas of Triangular Faces} \, . \end{equation*} \]
By substituting the calculated values for the base area and the areas of the triangular faces, we can obtain the total surface area of the pyramid. This value represents the sum of the areas of all the surfaces that make up the pyramid.
Practical Application and Real-World Significance
The ability to calculate the surface area of a pyramid has practical applications in various fields. Architects and engineers rely on this knowledge to design and construct stable and aesthetically pleasing structures. Additionally, understanding surface area calculations is crucial in fields such as construction, engineering, and even in the design of packaging and containers.
In conclusion, calculating the surface area of a pyramid involves a systematic approach that considers the shape of the base and the areas of the triangular faces. By applying the appropriate formulas and measuring the necessary dimensions, we can determine the total surface area of any pyramid. This knowledge not only contributes to our understanding of geometric concepts but also has real-world applications in various industries. So, the next time you encounter a pyramid, whether it’s a majestic ancient structure or a simple geometric model, you’ll have the tools to uncover its surface area secrets!
Expert Insight:

Dr. Emily Thompson, a renowned mathematician and geometry enthusiast, shares her perspective on the importance of surface area calculations:
“Surface area calculations are fundamental in understanding the spatial characteristics of objects. The ability to accurately determine the surface area of a pyramid opens up a world of possibilities in architectural design, engineering, and even art. It allows us to appreciate the intricate beauty of pyramids and their unique contributions to our built environment.”