Mastering the Art of Surface Area: Cylinder Secrets
The cylinder, a seemingly simple geometric shape, holds within its curves a world of mathematical intrigue and practical applications. From ancient architectural marvels to modern engineering feats, the concept of surface area has played a pivotal role in shaping our world. In this exploration, we delve into the intricacies of cylindrical surface area, unraveling the secrets that make this geometric concept a cornerstone of design and innovation.
At its core, the surface area of a cylinder represents the total area of its curved side and the areas of its circular ends. This seemingly straightforward definition, however, masks a complexity that has challenged mathematicians and engineers alike. The journey into the heart of cylindrical surface area reveals a blend of mathematical elegance and real-world functionality.
A Historical Perspective: Unraveling the Ancient Mystery

The concept of surface area, particularly as it relates to cylinders, has a rich history dating back to ancient civilizations. Early architects and engineers, despite their lack of modern mathematical tools, possessed an intuitive understanding of the practical implications of surface area. Take, for instance, the ancient Egyptians, whose mastery of geometry is evident in the precision of their monumental constructions.
Consider the Great Pyramid of Giza, a marvel of ancient engineering. While the pyramid’s shape is not cylindrical, the principles of surface area calculation were undoubtedly considered in its construction. The precise angles and measurements required to create such a structure demand an understanding of the area that encompasses the outer surface. This early application of surface area concepts highlights the practical importance of mathematical principles in tangible, real-world contexts.
The Evolution of Surface Area Calculations

As mathematics evolved, so too did the methods for calculating surface area. The ancient Greeks, notably Archimedes, made significant contributions to the field of geometry. Archimedes’ work, often considered the foundation of integral calculus, provided a deeper understanding of surface area and volume. His treatise on the measurement of a circle, for example, laid the groundwork for more precise calculations of cylindrical surface area.
The Middle Ages saw further advancements, with mathematicians like Leonardo da Vinci and Gerolamo Cardano building upon the work of their predecessors. Da Vinci, known for his diverse talents, applied mathematical principles to his artistic and engineering pursuits. His studies of the properties of solids, including cylinders, demonstrate a deep appreciation for the interplay between mathematics and the physical world.
Modern Applications: Cylindrical Surface Area in Action
In today’s world, the concept of cylindrical surface area has numerous practical applications across various industries.
Architecture and Design
Architects and designers utilize cylindrical shapes in a variety of contexts, from structural elements in buildings to artistic installations. Understanding the surface area of cylinders is crucial for ensuring structural integrity and optimizing material usage. For instance, in the design of water tanks or silos, precise calculations of surface area are essential to determine the required amount of material and ensure the structure’s stability.
Packaging and Product Design
The packaging industry relies heavily on cylindrical shapes for a wide range of products, from cans and bottles to tubes and containers. The surface area of these cylinders plays a critical role in determining the amount of material needed for production, as well as the overall cost and environmental impact of the packaging.
Engineering and Manufacturing
Engineers involved in manufacturing processes often work with cylindrical components, such as pipes, rods, and barrels. Accurate calculations of surface area are essential for ensuring efficient material utilization, minimizing waste, and optimizing production costs. Additionally, surface area considerations are vital in the design of heat exchangers, where efficient heat transfer relies on the proper surface area-to-volume ratio.
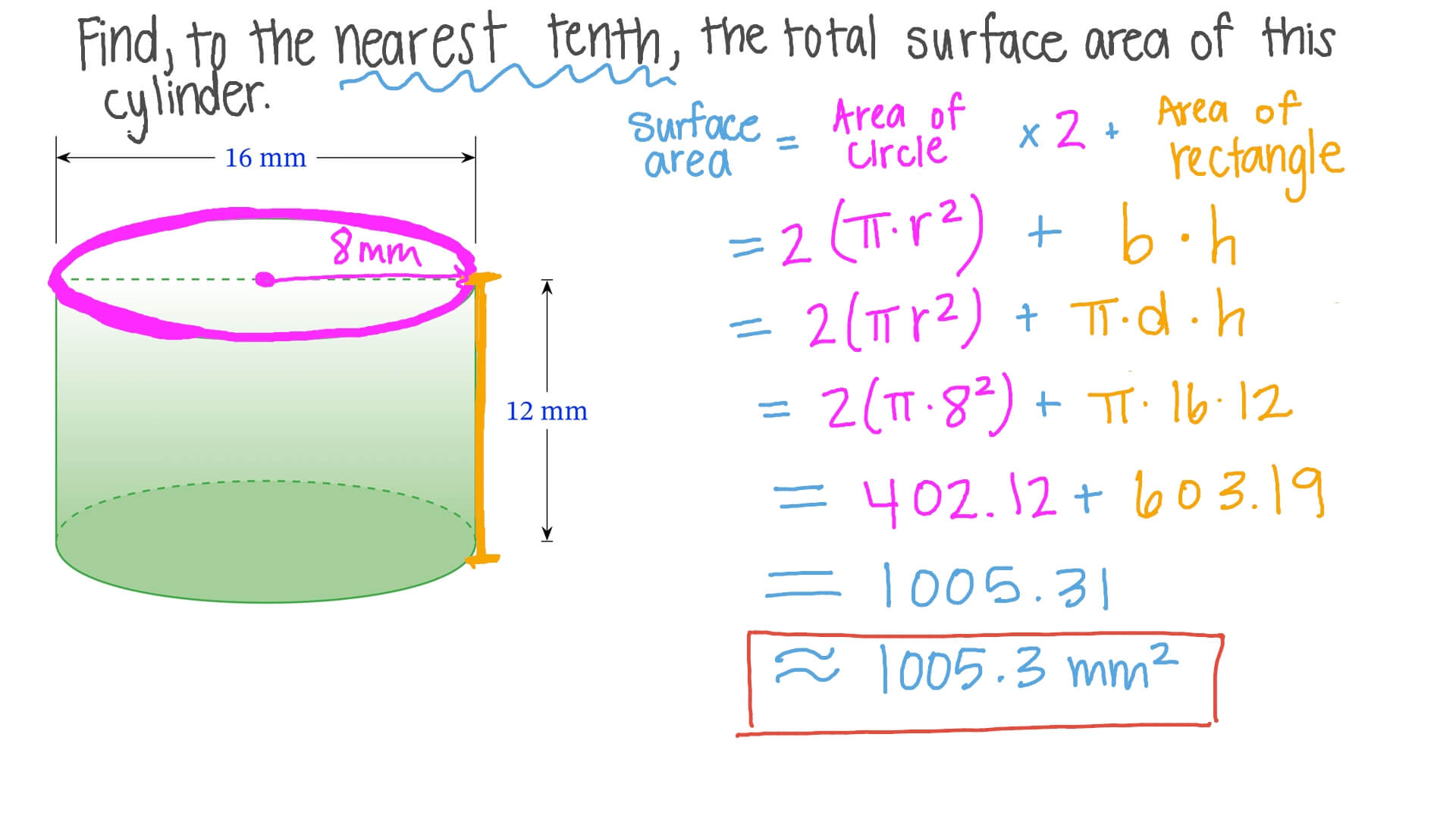
Unlocking the Secrets: A Step-by-Step Guide
Calculating the surface area of a cylinder involves a straightforward formula, yet its application requires precision and an understanding of the underlying principles.
Step 1: Understanding the Components
The surface area of a cylinder is comprised of two components: the area of the curved side and the areas of the circular ends. The curved side, often referred to as the lateral surface, can be calculated using the formula:
\[ \text{Lateral Surface Area} = 2\pi rh \]
where r is the radius of the base circle and h is the height of the cylinder.
The areas of the circular ends, or bases, can be calculated using the formula for the area of a circle:
\[ \text{Area of Base} = \pi r^2 \]
Step 2: Putting It All Together
To find the total surface area of the cylinder, we simply add the lateral surface area to twice the area of one base:
\[ \text{Total Surface Area} = 2\pi rh + 2\pi r^2 \]
This formula provides a concise representation of the surface area, but it is essential to recognize the underlying principles. The lateral surface area represents the curved side of the cylinder, which is essentially a rectangle with one side curved, while the bases are simple circles.
Real-World Example: Designing an Efficient Water Tank

Let’s consider a practical scenario to illustrate the application of cylindrical surface area calculations. Imagine you are tasked with designing a water tank for a rural community. The tank needs to be cylindrical to ensure even distribution of pressure, and it must be constructed using locally sourced materials.
Given the following specifications:
- Radius of the base circle (r): 2 meters
- Height of the cylinder (h): 4 meters
We can calculate the surface area of the water tank using the formula:
\[ \begin{align*} \text{Total Surface Area} &= 2\pi rh + 2\pi r^2 \\ &= 2\pi (2 \text{ m})(4 \text{ m}) + 2\pi (2 \text{ m})^2 \\ &= 16\pi \text{ m}^2 + 8\pi \text{ m}^2 \\ &= 24\pi \text{ m}^2 \text{ or approximately } 75.4 \text{ m}^2 \end{align*} \]
So, the total surface area of the water tank is approximately 75.4 \text{ square meters}. This calculation provides valuable insight into the amount of material required for construction, allowing for efficient procurement and cost estimation.
Conclusion: The Enduring Relevance of Cylindrical Surface Area
From ancient architectural wonders to modern manufacturing processes, the concept of cylindrical surface area has stood the test of time. Its application transcends mathematical theory, finding practical relevance in a myriad of fields. As we continue to innovate and push the boundaries of design and engineering, the understanding and calculation of surface area will remain a fundamental tool in our arsenal.
In the world of geometry, the cylinder’s surface area may not be the most complex or visually stunning, but its utility and practical implications make it a cornerstone of mathematical and scientific exploration.
Frequently Asked Questions:
What is the difference between lateral surface area and total surface area in the context of cylinders?
+The lateral surface area refers specifically to the curved side of the cylinder, while the total surface area encompasses both the lateral surface and the areas of the circular bases.
Can the surface area of a cylinder be calculated without knowing its height?
+No, the height of the cylinder is a critical component in the surface area calculation. It determines the length of the curved side, which is essential for finding the lateral surface area.
Are there any real-world applications where the surface area of a cylinder is irrelevant or unimportant?
+While the surface area of a cylinder is often crucial in design and engineering, there are scenarios where it may not be a primary consideration. For example, in the design of certain types of machinery or vehicles, the internal volume and shape may be more critical than the external surface area.
How does the surface area of a cylinder compare to that of other geometric shapes, such as spheres or cubes?
+The surface area of a cylinder is generally less than that of a sphere with the same radius and height, but more than that of a cube with the same volume. This comparison highlights the unique properties of each shape and their respective advantages in different applications.
Can the surface area of a cylinder be optimized to minimize material usage in certain applications?
+Yes, by manipulating the dimensions of a cylinder, such as its height or radius, it is possible to optimize its surface area for specific applications. This optimization often involves trade-offs between surface area and other factors like volume or structural integrity.