Unraveling the Mystery of Square Roots

Diving into the realm of square roots, we uncover a fundamental concept that shapes the very foundation of mathematics. It is a mathematical operation that has intrigued and challenged mathematicians for centuries, offering a fascinating journey into the heart of numbers. In this exploration, we will delve into the essence of square roots, understanding their origins, applications, and the mysteries they unravel in the world of mathematics.
At its core, a square root is a number that, when multiplied by itself, yields the original number. For instance, the square root of 9 is 3, as 3 multiplied by 3 equals 9. This simple concept, however, holds profound implications and applications across various mathematical disciplines.
The Historical Evolution of Square Roots

The concept of square roots has a rich historical lineage, with traces of its exploration dating back to ancient civilizations. In ancient Egypt, for instance, the concept of square roots was understood and applied in their measurement systems and architectural designs. The Egyptians used a method known as the ‘method of false position’ to estimate square roots, showcasing their early grasp of this mathematical operation.
Moving forward to ancient Greece, we find the works of Pythagoras and his school, who made significant contributions to the understanding of square roots. Pythagoras and his followers saw numbers and mathematical concepts as more than just tools for calculation; they were imbued with spiritual and philosophical meanings. Square roots, in their view, represented a connection between the physical and the divine, a concept that shaped their mathematical explorations.
The Greeks further developed methods for calculating square roots, such as the ‘Babylonian method’, which involved iterative approximations. This method, while not as precise as modern techniques, demonstrated the practical applications of square roots in geometry and architecture.
The Mathematical Significance of Square Roots

Square roots hold immense significance in the realm of mathematics, particularly in the field of algebra. They are essential in solving equations and understanding the behavior of functions. For instance, when solving quadratic equations, square roots play a pivotal role in determining the roots or solutions of the equation.
Moreover, square roots are deeply intertwined with complex numbers, a fascinating branch of mathematics that extends the concept of numbers beyond the real and imaginary planes. Complex numbers, which are expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, often involve square roots in their representation and operations.
Applications of Square Roots in the Real World
The practical applications of square roots extend far beyond the confines of mathematics. In physics, square roots are used in calculating the wavelengths of electromagnetic waves, a fundamental concept in understanding the behavior of light and other forms of radiation.
In engineering and architecture, square roots are essential in designing structures and systems. From calculating the dimensions of a building’s foundation to determining the optimal shape of an aircraft wing, square roots play a critical role in ensuring the stability and functionality of these structures.
Furthermore, square roots find applications in finance and economics. In portfolio management, for instance, square roots are used in calculating the standard deviation of investment returns, a crucial metric in assessing risk and making informed investment decisions.
Unraveling the Mystery: A Step-by-Step Guide
Understanding square roots can seem daunting, but with a structured approach, it becomes more accessible. Here’s a step-by-step guide to unraveling the mystery of square roots:
Step 1: Understand the Concept
Begin by grasping the fundamental definition of a square root. Remember, a square root is a number that, when multiplied by itself, yields the original number. For example, the square root of 25 is 5, as 5 x 5 equals 25.
Step 2: Practice with Basic Numbers
Start with simple numbers and practice finding their square roots. This helps build a solid foundation and improves your understanding of the concept. For instance, find the square roots of 4, 9, 16, and 25.
Step 3: Explore Square Roots of Non-Perfect Squares
Move on to numbers that are not perfect squares, such as 8 or 12. While these numbers don’t have whole number square roots, they can be expressed as decimal approximations. For example, the square root of 8 is approximately 2.828, and the square root of 12 is approximately 3.464.
Step 4: Apply Square Roots in Equations
Square roots are often encountered in algebraic equations. Practice solving equations that involve square roots, such as finding the value of x in the equation x^2 = 16.
Step 5: Understand Complex Numbers
Square roots are closely related to complex numbers. Explore the concept of complex numbers and how they are expressed and operated on using square roots. This opens up a whole new dimension in understanding numbers and their applications.
Key Takeaways
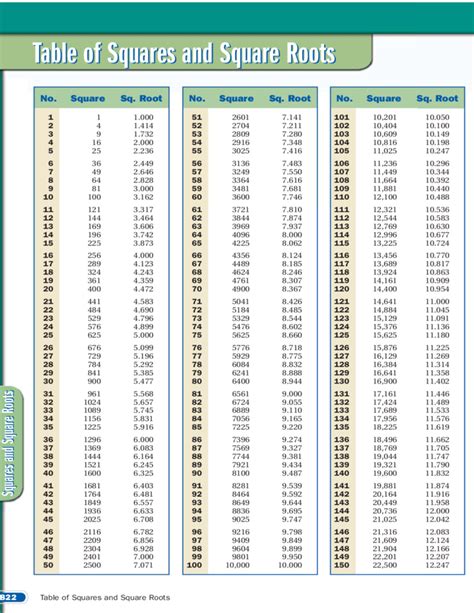
- Square roots are fundamental mathematical operations that involve finding a number that, when multiplied by itself, yields the original number.
- The concept of square roots has a rich historical lineage, with ancient civilizations like Egypt and Greece making significant contributions to its understanding.
- Square roots hold immense significance in algebra, helping to solve equations and understand the behavior of functions.
- The applications of square roots extend beyond mathematics, finding practical use in fields like physics, engineering, architecture, finance, and economics.
- Understanding square roots involves a structured approach, starting with basic numbers and gradually moving on to more complex applications and concepts.
Further Exploration and Resources
For those eager to delve deeper into the world of square roots, there are numerous resources available:
- Explore online courses and tutorials that offer comprehensive guides to understanding square roots and their applications.
- Engage with mathematical communities and forums where experts and enthusiasts discuss advanced topics related to square roots and their real-world applications.
- Read books and research papers by renowned mathematicians and scholars who have made significant contributions to the understanding and applications of square roots.
In conclusion, the mystery of square roots is a captivating journey into the heart of mathematics. From its ancient origins to its modern-day applications, square roots continue to shape our understanding of numbers and their profound impact on various disciplines. By unraveling this mystery, we gain a deeper appreciation for the beauty and complexity of mathematics.
What is the square root of a number?
+The square root of a number is a value that, when multiplied by itself, equals the original number. For example, the square root of 16 is 4, as 4 x 4 equals 16.
How are square roots used in real-world applications?
+Square roots find applications in various fields. In physics, they are used in calculating wavelengths. In engineering and architecture, they are essential for designing structures. In finance, they help assess investment risks. These are just a few examples of the diverse applications of square roots.
Can square roots be negative?
+Yes, square roots can be negative. While the principal square root of a number is always positive, there is also a negative square root. For example, the square root of 9 is both 3 and -3, as both values multiplied by themselves equal 9.
How do I calculate square roots manually?
+Calculating square roots manually involves a process known as the ‘Babylonian method’. This method involves iterative approximations, gradually refining the estimate until the desired level of accuracy is achieved. While time-consuming, it is a valuable skill to learn for understanding the concept.