Split Numbers: Divide Range into Equal Parts
The concept of splitting numbers into equal parts is a fundamental mathematical operation with practical applications in various fields. Whether you're an engineer, a data analyst, or simply someone interested in mathematics, understanding how to divide a range of numbers into equal parts can be incredibly useful. This article aims to provide an in-depth guide to this technique, covering its theoretical basis, practical applications, and real-world examples.
Understanding the Concept of Split Numbers

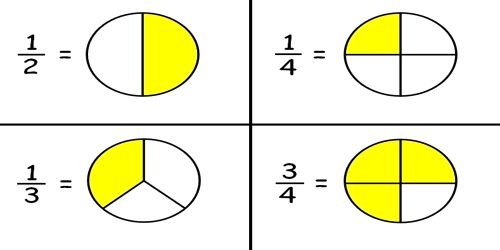
At its core, the idea of splitting numbers into equal parts involves dividing a given range of numbers into a specified number of intervals or groups, ensuring that each interval contains an equal number of elements. This operation is often referred to as “dividing a range” or “splitting a range into equal parts.” The key objective is to distribute the elements evenly across the specified number of intervals, ensuring a balanced distribution.
Mathematically, this operation can be expressed as follows: Given a range of numbers [a, b], where 'a' represents the starting point and 'b' represents the endpoint, and a positive integer 'n' representing the number of intervals, we want to find 'n' equally spaced points 'x1, x2, ..., xn' such that a = x1 < x2 < ... < xn = b.
Example:
Let’s say we have a range of numbers from 10 to 50, and we want to split this range into 4 equal parts. The calculated intervals would be: [10, 20), [20, 30), [30, 40), and [40, 50]. Each interval has a length of 10, ensuring an equal distribution of the numbers within the range.
Methods to Divide a Range into Equal Parts
There are several methods to achieve this division, each with its own advantages and use cases. Let’s explore some of the most common approaches:
1. Arithmetic Progression
Arithmetic progression is a straightforward method where the difference between consecutive terms (the common difference) is constant. In this method, we simply calculate the common difference and use it to find the intervals.
Formula: Common Difference (d) = (b - a) / n
| Range | Number of Parts (n) | Common Difference (d) | Intervals |
|---|---|---|---|
| [10, 50] | 4 | 10 | [10, 20), [20, 30), [30, 40), [40, 50) |
| [-5, 15] | 5 | 4 | [-5, 0), [0, 4), [4, 8), [8, 12), [12, 15) |

2. Geometric Progression
Geometric progression is useful when dealing with exponential growth or decay. Here, the ratio between consecutive terms (the common ratio) is constant.
Formula: Common Ratio (r) = (b / a)^(1/n)
| Range | Number of Parts (n) | Common Ratio (r) | Intervals |
|---|---|---|---|
| [1, 100] | 3 | sqrt(100) = 10 | [1, 10), [10, 100) |
| [2, 1024] | 5 | 64^(1/5) ≈ 3.31 | [2, 7), [7, 24), [24, 80), [80, 274), [274, 1024) |
3. Linear Interpolation
Linear interpolation is a more flexible method that allows for a smooth distribution of values within the range. It’s particularly useful when the endpoints of the range have specific values that need to be preserved.
Formula: xk = a + k * ((b - a) / n)
| Range | Number of Parts (n) | Intervals | |
|---|---|---|---|
| [10, 50] | 4 | x1 = 10 + 1 * (40 / 4) = 10 + 10 = 20 | [10, 20), [20, 30), [30, 40), [40, 50) |
| [0, 100] | 3 | x1 = 0 + 1 * (100 / 3) = 0 + 33.33, x2 = 0 + 2 * (100 / 3) = 0 + 66.67 | [0, 33.33), [33.33, 66.67), [66.67, 100) |
Real-World Applications
The technique of splitting numbers into equal parts has a wide range of practical applications across various fields. Here are some notable examples:
1. Data Analysis and Visualization
In data analysis, dividing data into equal intervals is crucial for creating histograms, bar charts, and other visualizations. This allows for a better understanding of the distribution of data and can reveal patterns or anomalies.
2. Engineering and Design
Engineers often use this technique to evenly distribute loads, design systems with equalized components, or plan construction projects with equal spacing.
3. Financial Planning
Financial advisors and investors use equal-interval splitting to create balanced investment portfolios, ensuring that each investment type or asset class has an equal allocation.
4. Software Development
In software, splitting a range into equal parts is used for data partitioning, load balancing, and even for generating test data with a specific distribution.
Conclusion
The ability to divide a range of numbers into equal parts is a powerful mathematical tool with a wide array of applications. Whether you’re analyzing data, designing systems, or simply solving mathematical problems, understanding these methods can greatly enhance your problem-solving skills. By mastering these techniques, you can approach complex problems with a systematic and efficient mindset.
Can this technique be used for non-numeric data?
+
While the primary focus of this article is on numeric data, the concept of splitting into equal parts can be extended to non-numeric data as well. For example, you could use this technique to evenly distribute tasks among team members or allocate resources across different departments.
What if the range has a non-integer endpoint?
+
In such cases, the methods described above might need slight adjustments. For instance, with linear interpolation, you might need to round the calculated values to the nearest integer. Geometric progression might be more suitable when dealing with non-integer endpoints, especially if the range exhibits exponential behavior.
Are there online tools or software that can help with this division?
+
Yes, there are various online calculators and software tools available that can assist with dividing a range into equal parts. These tools can automate the calculations and provide visual representations of the intervals. Some popular options include Excel functions, Python libraries, and web-based calculators.