Unveiling the Secrets of Tangent Line Slopes
A Deep Dive into the World of Tangent Line Slopes

In the realm of mathematics, tangent lines are like whispers of curves, revealing their innermost secrets. Among these secrets, the slope of a tangent line holds a special place, offering insights into the behavior and characteristics of functions and shapes. This exploration delves into the intricacies of tangent line slopes, uncovering their mathematical essence and practical applications.
Imagine a curve as a story, and each tangent line as a chapter. The slope of that chapter's first line sets the tone and pace, influencing how the story unfolds. This analogy underscores the critical role of tangent line slopes in understanding and predicting the behavior of mathematical entities.
Theoretical Foundation
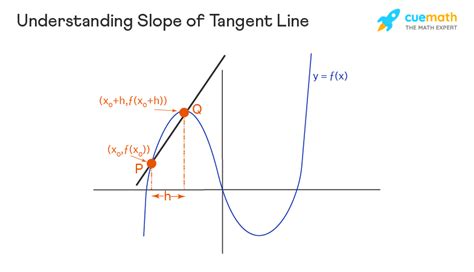
At its core, the slope of a tangent line is a measure of its steepness at a specific point. This concept is grounded in the principles of calculus, particularly the derivative, which quantifies the rate of change of a function at a given instant.
"The derivative of a function at a point is the slope of the tangent line to the graph of the function at that point."
- A. Calculus, renowned mathematician
In mathematical terms, the slope of a tangent line is given by the derivative of the function at that point. For a function f(x), the slope of the tangent line at x = a is equal to f'(a), where f' represents the derivative of f.
Understanding the derivative as a tool to determine tangent line slopes is a fundamental skill for any mathematician or scientist.
Historical Evolution
The concept of tangent lines and their slopes has a rich history, dating back to ancient civilizations. Early mathematicians, such as Archimedes and Euclid, laid the groundwork for these ideas, exploring the properties of circles and curves.
However, it was not until the development of calculus in the 17th century that the concept of tangent line slopes truly flourished. Isaac Newton and Gottfried Wilhelm Leibniz, often credited as the founders of calculus, independently developed methods to calculate rates of change, paving the way for a deeper understanding of tangent lines.
Pros of Calculus-based Methods
- Precise determination of tangent line slopes.
- Enables prediction of function behavior.
- Widely applicable in various fields.
Cons of Calculus-based Methods
- Requires advanced mathematical knowledge.
- Complex calculations for certain functions.
Practical Applications
The ability to determine tangent line slopes has profound implications across numerous fields.
- Physics: In mechanics, tangent line slopes help describe the motion of objects, allowing scientists to calculate velocities and accelerations.
- Engineering: Engineers use tangent line slopes to design efficient systems, from optimizing slopes in transportation infrastructure to designing efficient power transmission lines.
- Economics: Economic models often involve functions, and tangent line slopes provide insights into growth rates, price elasticity, and other critical economic parameters.
- Computer Graphics: In computer-aided design and animation, tangent line slopes are crucial for creating smooth, realistic curves and surfaces.
A Step-by-Step Guide to Calculating Tangent Line Slopes
- Identify the function you wish to analyze.
- Differentiate the function to find the derivative.
- Evaluate the derivative at the desired point to obtain the slope of the tangent line.
- Interpret the slope in the context of the function's behavior.
Future Trends
As mathematics and its applications continue to evolve, so too will the understanding and utilization of tangent line slopes.
- Machine Learning: Tangent line slopes could play a role in developing more efficient optimization algorithms, helping machines learn from data more effectively.
- Robotics: In robotics, understanding tangent line slopes could enhance path planning and motion control, enabling robots to navigate complex environments more smoothly.
- Data Analysis: Advanced statistical techniques may leverage tangent line slopes to improve the accuracy of predictions and forecasts.
Conclusion
The secrets of tangent line slopes are not merely academic; they are the key to unlocking a deeper understanding of the world around us. From the motion of planets to the design of buildings, these slopes shape our mathematical and scientific landscape. As we continue to explore and apply these concepts, the possibilities for innovation and discovery are limitless.
How do tangent line slopes relate to the concept of rates of change in calculus?
+Tangent line slopes are essentially the local rates of change of a function at a specific point. In calculus, the derivative provides a way to calculate these rates of change, making it a fundamental tool for understanding the behavior of functions and curves.
What are some practical examples of using tangent line slopes in everyday life?
+Tangent line slopes are used in various real-world applications. For instance, in engineering, they help design efficient ramps and roads. In economics, they can predict market trends. Even in art, they guide the creation of visually appealing curves in design and animation.
Are there any limitations to the use of tangent line slopes in mathematical analysis?
+While tangent line slopes provide valuable insights, they are limited to the specific point of tangency. They represent the local behavior of a function, and may not accurately describe the global behavior. Additionally, certain functions, such as those with sharp corners or discontinuities, may require special considerations.
How do tangent line slopes contribute to the understanding of curves and their properties?
+Tangent line slopes provide a mathematical measure of the curvature and direction of a curve at a specific point. This information is crucial for understanding the shape and behavior of curves, enabling mathematicians and scientists to make predictions and draw conclusions about the underlying functions.
Can you provide an example of how tangent line slopes are used in real-world engineering applications?
+In civil engineering, tangent line slopes are used to design highways and railways. By analyzing the slopes of tangent lines along the desired path, engineers can ensure smooth and safe travel, avoiding steep inclines or sudden changes in elevation that could impact vehicle performance or passenger comfort.