Mathematical Secrets: 5 Insights on Sin π/2
The mathematical constant π, often referred to as pi, is a fundamental concept in mathematics, known for its endless decimal representation and its central role in various fields of study. One of the intriguing aspects of π is the behavior of trigonometric functions at specific angles, and among these, the value of sin π/2 holds a special place. Let’s delve into five insights that reveal the mathematical secrets behind this seemingly simple expression.
1. The Concept of Trigonometric Functions and Their Periodicity
To understand the significance of sin π/2, we must first explore the world of trigonometric functions. Trigonometry, a branch of mathematics that deals with the relationships between the sides and angles of triangles, introduces us to functions like sine, cosine, and tangent. These functions are periodic, meaning they repeat their values at regular intervals. In the case of sine and cosine, the period is 2π, which represents a full revolution or a complete cycle.
The sine function, in particular, oscillates between -1 and 1 as the angle varies. It reaches its maximum value of 1 at π/2, commonly known as a right angle or a quarter turn. This angle holds a special place in trigonometry and is often the starting point for many mathematical explorations.
2. The Intriguing Value of Sin π/2
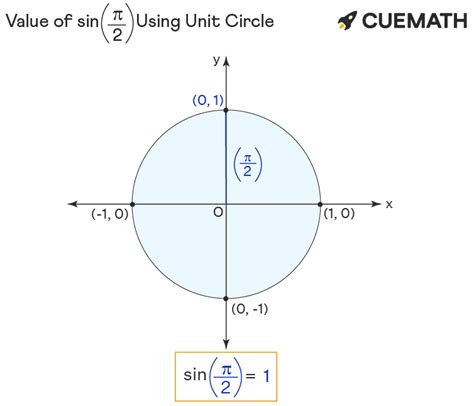
When we evaluate the sine function at π/2, we encounter a fascinating value. The expression sin π/2 equals exactly 1. This value is not just a random occurrence but holds deep mathematical significance. It represents the fact that a right angle, or π/2 radians, corresponds to the highest positive value the sine function can attain.
Imagine a unit circle, a circle with a radius of 1 centered at the origin. As we move along the circle, starting from the positive x-axis, we encounter the point (1, 0), which corresponds to an angle of 0 radians. As we continue our journey counterclockwise, we reach the point (0, 1) at π/2 radians. This point on the unit circle represents the maximum positive value of the sine function, and thus, sin π/2 equals 1.
3. The Relationship Between Trigonometric Functions and the Unit Circle
The unit circle is a powerful tool in trigonometry, providing a visual representation of the relationships between angles and trigonometric functions. By plotting the values of sine and cosine on the unit circle, we can observe their periodic behavior and understand their connection to angles.
When we consider the point (0, 1) on the unit circle, which corresponds to π/2 radians, we see that the y-coordinate represents the value of sin π/2. This point is located at the top of the circle, indicating that the sine function reaches its maximum positive value at this angle. Conversely, the point (-1, 0) on the opposite side of the circle represents an angle of 3π/2, where the sine function takes on its maximum negative value of -1.
4. Historical Significance and Applications
The concept of sin π/2 has historical roots dating back to ancient civilizations. Early mathematicians, such as the Babylonians and Egyptians, recognized the importance of right angles and their relationship to trigonometric functions. They developed practical applications for trigonometry, including measuring distances and angles in construction and astronomy.
In modern times, trigonometric functions, including sine, are ubiquitous in various scientific and engineering disciplines. From navigating satellites to designing sound systems, the understanding of sin π/2 and its counterparts plays a crucial role. It is a fundamental building block in fields like physics, engineering, and computer graphics, where precise calculations and simulations rely on accurate trigonometric values.
5. Beyond Sin π/2: Exploring Other Trigonometric Identities
While sin π/2 is a fascinating starting point, the world of trigonometry extends far beyond this specific value. Trigonometric identities, equations involving trigonometric functions that hold true for all angles, provide a deeper understanding of these mathematical relationships.
For example, the Pythagorean identity, sin^2(θ) + cos^2(θ) = 1, is a fundamental identity that connects the sine and cosine functions. This identity, along with other trigonometric identities, allows us to manipulate and transform expressions involving trigonometric functions, leading to powerful mathematical insights and applications.
In conclusion, the value of sin π/2, equal to 1, reveals a fundamental aspect of trigonometry. It showcases the periodic nature of trigonometric functions and their connection to angles. Understanding this value and its implications provides a solid foundation for exploring the vast landscape of trigonometry and its applications in various fields. As we continue to unravel the mathematical secrets of sin π/2 and other trigonometric concepts, we gain a deeper appreciation for the beauty and complexity of mathematics.
What is the practical significance of understanding sin π/2 in everyday life?
+Understanding sin π/2 and trigonometric functions in general has practical applications in fields like architecture, engineering, and navigation. For instance, architects use trigonometry to design structures with precise angles and dimensions, ensuring stability and aesthetic appeal. Engineers rely on trigonometric principles to analyze and design mechanical systems, while navigators use trigonometry to calculate distances and angles for accurate navigation.
Are there other angles besides π/2 where the sine function takes on significant values?
+Absolutely! Trigonometric functions exhibit interesting behaviors at various angles. For example, sin 0 equals 0, indicating that the sine function starts at the origin and gradually increases as the angle increases. Additionally, sin π equals 0, marking the completion of one full revolution or a full cycle of the sine function. These significant values at specific angles provide valuable insights into the periodic nature of trigonometric functions.
How does the concept of sin π/2 relate to the unit circle in a practical sense?
+The unit circle provides a visual representation of trigonometric functions, including sine. When we consider the point (0, 1) on the unit circle, which corresponds to π/2 radians, we see that the y-coordinate represents the value of sin π/2. This point is located at the top of the circle, indicating the maximum positive value of the sine function. The unit circle allows us to visualize and understand the relationship between angles and trigonometric functions in a tangible way.
Can trigonometric functions like sin π/2 be used in complex mathematical calculations?
+Absolutely! Trigonometric functions, including sine, are integral to various mathematical calculations and models. They play a crucial role in fields like physics, engineering, and computer graphics, where precise trigonometric values are essential for accurate simulations and predictions. For example, in physics, trigonometric functions are used to describe the motion of objects and the behavior of waves.



