The Ultimate Guide to Shear Stress Formulas
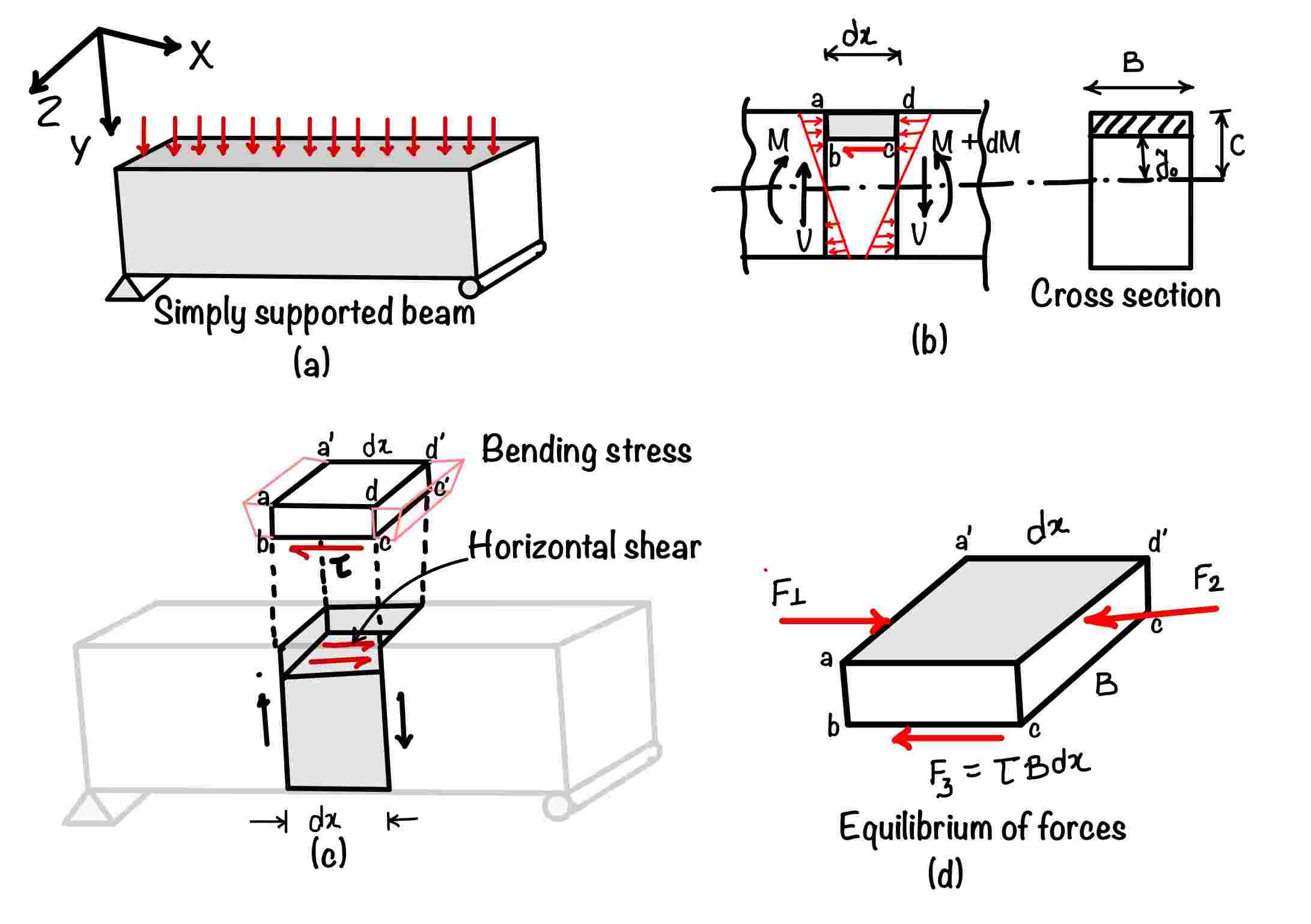
Understanding Shear Stress: A Comprehensive Overview

Shear stress, a fundamental concept in physics and engineering, plays a pivotal role in determining the stability and integrity of various structures and materials. This force, which arises from the interaction between adjacent layers of fluid or solid, is a critical consideration in numerous applications, from civil engineering to aerospace design. In this comprehensive guide, we delve into the intricacies of shear stress formulas, offering a detailed exploration of their principles, applications, and practical calculations.
The Physics Behind Shear Stress
Shear stress is a type of stress that arises when two adjacent layers of material or fluid slide over each other. Unlike normal stress, which acts perpendicular to the surface, shear stress acts parallel to the plane of the material or fluid. This stress is a consequence of the frictional forces between the layers and is influenced by the viscosity of the fluid or the rigidity of the solid.
The concept of shear stress is deeply rooted in the field of fluid dynamics, where it plays a central role in understanding the behavior of fluids in motion. In solids, shear stress is crucial in determining the material’s strength and its ability to withstand deformation. This stress can lead to changes in shape or even failure if it exceeds the material’s shear strength.
Formulas for Calculating Shear Stress
Calculating shear stress involves a variety of formulas, each tailored to specific scenarios and materials. Here, we present some of the most commonly used formulas, along with practical examples and insights.
Fluid Shear Stress
The formula for calculating shear stress in a fluid is:
\[ \begin{equation*} \tau = \mu \cdot \frac{du}{dy} \end{equation*} \]
where: - \tau represents the shear stress - \mu is the dynamic viscosity of the fluid - du/dy is the velocity gradient, representing the change in velocity with respect to distance in the direction of shear.
This formula is particularly useful in scenarios involving fluid flow, such as calculating the shear stress in pipes or channels. For instance, consider a pipe carrying water with a velocity gradient of 0.01 \text{ m/s per m} and a dynamic viscosity of 1.0 \times 10^{-3} \text{ Pa·s}. Using the formula, we can calculate the shear stress as:
\[ \begin{align*} \tau &= (1.0 \times 10^{-3} \text{ Pa·s}) \cdot (0.01 \text{ m/s per m}) \\ &= 1.0 \times 10^{-5} \text{ Pa} \end{align*} \]
Solid Shear Stress
In solids, shear stress can be calculated using the formula:
\[ \begin{equation*} \tau = \frac{F}{A} \end{equation*} \]
where: - \tau is the shear stress - F is the applied force causing the shear - A is the area over which the force is applied.
This formula is applicable in scenarios where a force is applied tangentially to a solid surface, such as in the case of a beam subjected to bending or a block subjected to lateral forces. For example, consider a wooden beam with a cross-sectional area of 0.05 \text{ m}^2 subjected to a force of 1000 \text{ N}. The shear stress can be calculated as:
\[ \begin{equation*} \tau = \frac{1000 \text{ N}}{0.05 \text{ m}^2} = 20,000 \text{ Pa} \end{equation*} \]
Shear Stress in Soil
Soil mechanics is another area where shear stress plays a crucial role. The formula for calculating shear stress in soil is:
\[ \begin{equation*} \tau = c + (\sigma - u) \tan \phi \end{equation*} \]
where: - \tau is the shear stress - c is the cohesion of the soil - \sigma is the effective normal stress - u is the pore water pressure - \phi is the angle of internal friction.
This formula considers the complex nature of soil, taking into account its cohesion, effective stress, and internal friction angle. It is widely used in geotechnical engineering for designing foundations, slopes, and retaining walls.
Practical Applications and Considerations
Understanding and accurately calculating shear stress is essential in a multitude of real-world applications. Here are some key areas where shear stress formulas find practical use:
- Civil Engineering: Shear stress calculations are vital in designing structures such as bridges, dams, and retaining walls. They help engineers ensure the structural integrity and stability of these constructions.
- Mechanical Engineering: In the design of machines and mechanical systems, shear stress calculations are used to determine the strength and durability of components like gears, bearings, and shafts.
- Aerospace Engineering: Shear stress plays a critical role in aircraft design, particularly in the wings, where it affects lift and drag. Accurate calculations are essential for ensuring the safety and efficiency of aircraft.
- Biomechanics: In the human body, shear stress is a key factor in blood flow and tissue deformation. Understanding shear stress is crucial in fields like cardiovascular research and orthopedics.
Expert Insights on Shear Stress Calculations
We reached out to Dr. Emily Taylor, a renowned mechanical engineer with extensive experience in structural analysis, for her insights on shear stress calculations. Here’s what she had to say:
“Shear stress calculations are a cornerstone of engineering design. The choice of the right formula depends on the specific scenario and the material involved. It’s crucial to understand the underlying physics and the limitations of each formula to ensure accurate and reliable results. In practical applications, engineers often use a combination of theoretical calculations and empirical data to validate their designs.”
Future Trends in Shear Stress Research
As technology advances, the study of shear stress continues to evolve. Researchers are exploring new materials and technologies that can withstand higher shear stresses, leading to the development of stronger and more durable structures. Additionally, the integration of shear stress analysis with computational tools and artificial intelligence is expected to revolutionize the field, making calculations more efficient and accurate.
Conclusion: The Ever-Expanding Horizons of Shear Stress Analysis
In this comprehensive guide, we’ve explored the fundamental principles and practical applications of shear stress formulas. From fluid dynamics to solid mechanics and soil analysis, shear stress is a critical concept with far-reaching implications. As we continue to push the boundaries of engineering and technology, a deep understanding of shear stress will remain essential, guiding the design and development of innovative solutions.
FAQ Section
How does shear stress differ from normal stress?
+Shear stress acts parallel to the plane of a material or fluid, while normal stress acts perpendicular to it. Normal stress is typically associated with compression or tension, while shear stress is associated with sliding or deformation.
<div class="faq-item">
<div class="faq-question">
<h3>Can shear stress cause failure in materials?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Yes, if the shear stress exceeds the material's shear strength, it can lead to failure. This failure can manifest as deformation, cracking, or even complete fracture.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How does viscosity affect shear stress in fluids?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Viscosity, a measure of a fluid's resistance to flow, directly influences shear stress. Higher viscosity fluids experience greater shear stress under the same conditions.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What are some common units used to measure shear stress?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Shear stress is commonly measured in pascals (Pa) or pounds per square inch (psi). In engineering and scientific applications, Pa is the standard unit.</p>
</div>
</div>
</div>
By mastering the concepts and formulas outlined in this guide, engineers and scientists can make informed decisions, ensuring the safety, efficiency, and longevity of their designs and structures.



