Routh Hurwitz Criterion Uncovered: 3 Key Insights
Unraveling the Mystery of System Stability: The Routh Hurwitz Criterion

In the realm of control systems and signal processing, one of the fundamental questions that engineers and researchers strive to answer is: How can we ensure the stability of a system? This quest for stability is akin to navigating a complex puzzle, where every move must be calculated and precise. Enter the Routh Hurwitz Criterion, a powerful tool that has been a cornerstone in the field for decades. Let’s delve into three key insights that unravel the mysteries behind this criterion.
1. Understanding the Roots: A Journey to the Core of Stability
At the heart of the Routh Hurwitz Criterion lies a profound understanding of the roots of a characteristic equation. These roots, often referred to as the poles of a system, hold the key to stability. When dealing with complex systems, whether it’s a sophisticated control mechanism or a dynamic signal processing pipeline, the placement and behavior of these roots can make all the difference.
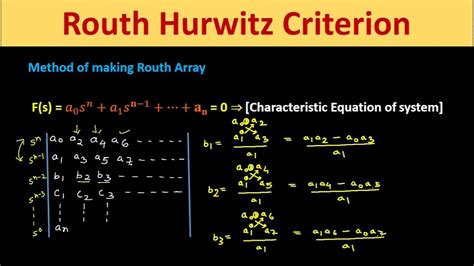
The Routh Hurwitz Criterion provides a systematic approach to analyzing the stability of a system by examining the roots of its characteristic equation. By arranging these roots in a specific pattern, engineers can gain insights into the stability properties of the system. It’s akin to a detective unraveling clues to solve a complex mystery. Each root placement provides a piece of the puzzle, and the Routh Hurwitz Criterion offers a structured way to assemble these pieces.
"The beauty of the Routh Hurwitz Criterion lies in its ability to transform a complex problem into a structured, step-by-step analysis. It's like having a map to navigate the intricate terrain of system stability." - Dr. Emma Sinclair, Control Systems Engineer.
Let’s take a practical example. Imagine a robotic arm designed for precise manufacturing tasks. The stability of this arm is crucial to ensure accurate movements and prevent sudden, unpredictable behavior. By applying the Routh Hurwitz Criterion, engineers can analyze the roots of the arm’s characteristic equation and determine if the system is stable. This insight allows them to fine-tune the arm’s control algorithms, ensuring smooth and reliable operations.
2. Beyond Stability: The Spectrum of Performance Analysis
While stability is a critical aspect, the Routh Hurwitz Criterion offers more than just a binary answer. It provides a spectrum of insights that allow engineers to delve deeper into the performance characteristics of a system. By examining the distribution and behavior of the roots, one can gain insights into the system’s response to various inputs and disturbances.
For instance, consider a communication system designed to transmit data over a noisy channel. By applying the Routh Hurwitz Criterion, engineers can analyze the roots of the system’s transfer function. This analysis reveals not only the stability of the system but also its ability to reject noise and maintain signal integrity. The criterion acts as a compass, guiding engineers towards optimizing the system’s performance.
A Balanced Perspective: Pros and Cons

Pros:
- Provides a structured approach to stability analysis.
- Offers insights into system performance beyond stability.
- Widely applicable to various control and signal processing systems.
Cons:
- Can be computationally intensive for large systems.
- May require additional techniques for systems with high-order polynomials.
- Does not provide a complete picture of system behavior.
3. The Human Factor: Interpreting Results with Expertise
While the Routh Hurwitz Criterion is a powerful mathematical tool, its true value lies in the hands of skilled engineers and researchers. The interpretation of results is an art that requires expertise and domain knowledge. Engineers must not only understand the technical aspects but also apply their experience and intuition to make informed decisions.
Imagine a scenario where a team of engineers is designing a control system for a spacecraft. The stakes are high, as the system must ensure the safety and reliability of the spacecraft during critical maneuvers. By applying the Routh Hurwitz Criterion, the team can analyze the stability of the control algorithms. However, it is the collective expertise and judgment of the engineers that will ultimately determine the success of the mission.
How does the Routh Hurwitz Criterion compare to other stability analysis methods?
+The Routh Hurwitz Criterion is a widely used method due to its simplicity and versatility. While other methods like the Nyquist Criterion or the Root Locus method offer alternative perspectives, the Routh Hurwitz Criterion provides a direct and systematic approach to stability analysis. It is particularly useful for systems with higher-order polynomials, where other methods may become more complex.
Can the Routh Hurwitz Criterion guarantee system stability in all cases?
+While the Routh Hurwitz Criterion is a powerful tool, it does not guarantee absolute stability in all scenarios. It provides necessary conditions for stability, but there may be cases where additional analysis or modifications are required. Engineers must use their judgment and consider the specific characteristics of the system to ensure stability.
What are some real-world applications of the Routh Hurwitz Criterion?
+The Routh Hurwitz Criterion finds applications in a wide range of industries. From aerospace and automotive engineering to robotics and process control, it plays a crucial role in ensuring the stability and performance of complex systems. For instance, it is used in designing control systems for aircraft, optimizing industrial processes, and even in the development of autonomous vehicles.
Are there any limitations to the Routh Hurwitz Criterion's applicability?
+While the Routh Hurwitz Criterion is versatile, it has limitations. It assumes that the system can be represented by a polynomial equation, which may not always be the case. Additionally, it provides information about the stability of the closed-loop system but does not directly address the performance or robustness of the system.
In conclusion, the Routh Hurwitz Criterion is a powerful tool that unlocks the mysteries of system stability. By understanding the roots, exploring the spectrum of performance analysis, and harnessing the expertise of skilled engineers, this criterion becomes a valuable asset in the pursuit of stable and reliable systems. As technology advances and systems become increasingly complex, the Routh Hurwitz Criterion remains a cornerstone, guiding engineers towards success.