Precision Rounding: 3 Simple Tips

Precision rounding is a vital technique in data analysis and scientific computing, allowing for the accurate and consistent representation of numerical values. In this article, we delve into the world of precision rounding, exploring its significance, the common challenges associated with it, and most importantly, we provide you with three simple yet effective tips to master this essential skill.
The Importance of Precision Rounding

Precision rounding plays a crucial role in various fields, including engineering, finance, and data science. It ensures that numerical data is presented accurately, reducing the chances of errors and misinterpretations. By rounding numbers to a specified precision, we can simplify complex calculations, improve data readability, and make informed decisions based on reliable data.
Imagine a scenario where a financial analyst is working on a portfolio with investments valued at $1,234,567.89. Representing this value with excessive precision might not be practical or necessary. Precision rounding allows the analyst to round the value to a more manageable and meaningful level, such as $1,234,568, without losing essential information.
Challenges in Precision Rounding
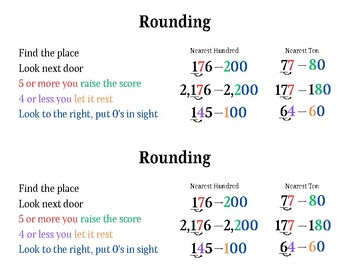
While precision rounding is a straightforward concept, it can present challenges, especially when dealing with large datasets or complex calculations. Some common issues include:
- Loss of Precision: Rounding numbers can lead to a loss of significant digits, especially when rounding to a lower precision. This can impact the accuracy of subsequent calculations.
- Consistency: Ensuring consistent rounding across different data sets or calculations is crucial. Inconsistent rounding practices can introduce errors and discrepancies.
- Rounding Methods: Choosing the appropriate rounding method is essential. Different methods, such as rounding up, down, or to the nearest value, can produce varying results and may not always be suitable for the specific context.
Tip 1: Understand the Significance of Precision
The first step towards mastering precision rounding is understanding the significance of precision in your specific domain or application. Consider the following questions:
- What level of precision is required for your data or calculations? Is it sufficient to round to the nearest whole number, or do you need a higher precision like two or three decimal places?
- Are there any industry standards or guidelines that dictate the precision level for your field? Adhering to these standards ensures consistency and facilitates communication with peers and clients.
- How will the loss of precision impact your analysis or decision-making process? Understanding the potential consequences helps you make informed choices when rounding numbers.
Real-World Example: Engineering Tolerances
In engineering, precision rounding is crucial when specifying tolerances for manufactured parts. For instance, when designing a mechanical component with a tight fit, engineers might need to specify dimensions with a precision of 0.01 mm. Rounding to a lower precision could result in parts that do not fit together properly, leading to functional issues or even failures.
Tip 2: Choose the Right Rounding Method
Selecting the appropriate rounding method is essential to ensure accurate and fair representation of your data. Here are some commonly used rounding methods and their applications:
- Rounding to the Nearest Value: This method is straightforward and often the default choice. It involves rounding a number to the nearest value based on a specified precision. For example, rounding 1.2345 to two decimal places would result in 1.23.
- Rounding Up or Down: In certain cases, it may be necessary to round up or down to ensure a conservative or optimistic estimate. For instance, when calculating costs, rounding up might be preferred to avoid underestimating expenses.
- Banker's Rounding: Banker's rounding, also known as symmetric rounding, is a method that rounds to the nearest even value. This method ensures that rounding errors are distributed evenly across both directions. It is commonly used in financial calculations to avoid bias.
- Custom Rounding Functions: In some programming languages or software tools, you can create custom rounding functions tailored to your specific needs. This allows for precise control over rounding behavior and can be particularly useful for complex calculations.
Comparative Analysis: Rounding Methods
To illustrate the impact of different rounding methods, let’s consider a simple example. We have a list of prices: 1.2345, 2.4678, and $3.6912. We want to round these prices to two decimal places using various methods:
| Price | Nearest Value | Round Up | Round Down | Banker's Rounding |
|---|---|---|---|---|
| $1.2345 | $1.23 | $1.24 | $1.23 | $1.23 |
| $2.4678 | $2.47 | $2.47 | $2.46 | $2.47 |
| $3.6912 | $3.69 | $3.69 | $3.69 | $3.69 |

As you can see, the choice of rounding method can lead to different outcomes, and it is essential to select the method that aligns with your specific requirements.
Tip 3: Implement Rounding Functions with Caution
When implementing rounding functions, whether built-in or custom, it is crucial to exercise caution to avoid potential errors or unexpected results. Consider the following tips:
- Test with Edge Cases: Test your rounding functions with a variety of edge cases, including numbers close to the rounding threshold. This helps identify any issues or unexpected behavior.
- Handle Negative Numbers: Ensure that your rounding functions handle negative numbers appropriately. Some rounding methods might need adjustments to work correctly with negative values.
- Document and Communicate: Document the rounding methods and functions used in your calculations. This documentation is essential for reproducibility and facilitates collaboration with colleagues.
- Consider Data Types: Be mindful of the data types used in your calculations. Rounding functions might behave differently with different data types, such as integers versus floating-point numbers.
Expert Insight: Rounding in Data Analysis
Conclusion
Precision rounding is a fundamental skill in data handling and analysis. By understanding the significance of precision, selecting the right rounding method, and implementing rounding functions with care, you can ensure accurate and reliable representation of your data. Remember, precision rounding is a tool to enhance the clarity and interpretability of your data, contributing to better decision-making and analysis.
How does precision rounding impact the accuracy of calculations?
+Precision rounding can impact calculation accuracy by introducing a loss of significant digits. While rounding simplifies numbers, it may lead to slight deviations from the original value. However, when chosen and applied correctly, precision rounding can provide a balanced trade-off between simplicity and accuracy.
Are there any best practices for rounding in scientific research?
+In scientific research, it is essential to maintain consistency and transparency in rounding practices. Researchers should clearly document the rounding methods used and provide justification for their choices. Additionally, when presenting results, it is good practice to indicate the level of precision used.
Can precision rounding be automated in programming languages?
+Yes, many programming languages provide built-in functions or libraries for precision rounding. These functions allow you to specify the precision level and the rounding method. However, it is crucial to understand the underlying behavior of these functions to avoid potential errors or unexpected results.