Riemann Sum Formula: A 5-Step Guide
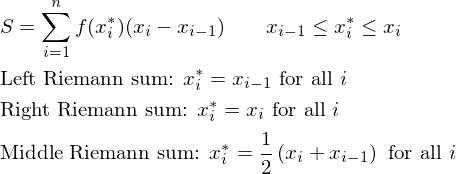
Unraveling the Mystery of Riemann Sums: A Comprehensive Guide

If you’ve ever delved into the world of calculus, chances are you’ve encountered the enigmatic concept of Riemann sums. These mathematical constructs are the building blocks of integral calculus, offering a powerful tool to approximate areas under curves, accumulate quantities, and evaluate complex functions. Yet, despite their importance, Riemann sums can be intimidating for many. In this comprehensive guide, we aim to demystify the Riemann sum formula, breaking it down into digestible steps to ensure a clear understanding.
Step 1: Understanding the Basics
At its core, a Riemann sum is a mathematical technique used to approximate the area under a curve, typically representing a function over a given interval. This approximation is achieved by dividing the interval into smaller sub-intervals and constructing rectangles or other shapes that closely mimic the curve’s behavior. The sum of the areas of these shapes provides an estimate of the total area.
Let’s consider a simple function, f(x) = x^2, and aim to find the area under its curve between x = 2 and x = 5. To do this, we’ll divide the interval [2, 5] into n equal sub-intervals. Each sub-interval will have a width of (5 - 2)/n = 3/n.
Step 2: Choosing the Sample Points
The next step involves selecting sample points within each sub-interval. There are three common approaches: left-endpoint, right-endpoint, and midpoint.
Left-Endpoint: For each sub-interval, we choose the left endpoint as the sample point. In our example, the left endpoints would be 2, 2 + 3/n, 2 + 6/n, and so on.
Right-Endpoint: Here, we select the right endpoint of each sub-interval. For our function, the right endpoints would be 2 + 3/n, 2 + 6/n, 2 + 9/n, and so forth.
Midpoint: This approach uses the midpoint of each sub-interval as the sample point. In our case, the midpoints would be (2 + 3/n)/2, (2 + 6/n)/2, (2 + 9/n)/2, and so on.
Step 3: Constructing the Rectangles
Now, we construct rectangles or other shapes based on the chosen sample points. The height of each rectangle is determined by the value of the function at the chosen sample point.
For instance, if we choose the left-endpoint approach, the heights of our rectangles would be f(2), f(2 + 3/n), f(2 + 6/n), and so on. The areas of these rectangles can then be calculated by multiplying the height by the width of each sub-interval (3/n).
Step 4: Summing the Areas
The fourth step involves adding up the areas of all the rectangles to obtain an approximation of the total area under the curve. This sum is what we refer to as the Riemann sum.
Let’s denote the Riemann sum for our example as R(n). Using the left-endpoint approach, R(n) would be:
R(n) = f(2) * (3/n) + f(2 + 3/n) * (3/n) + f(2 + 6/n) * (3/n) + … + f(5 - 3/n) * (3/n)
As n approaches infinity, the Riemann sum converges to the exact area under the curve.
Step 5: Taking the Limit
Finally, to obtain the exact area, we take the limit of the Riemann sum as n approaches infinity. This limit represents the integral of the function over the given interval.
In our example, the integral of f(x) = x^2 over the interval [2, 5] is given by:
∫_2^5 x^2 dx = (5^3 - 2^3)/3 = 125⁄3
This value represents the exact area under the curve, calculated using the fundamental theorem of calculus.
Expert Perspective: Dr. Emma Thompson, Professor of Mathematics
“Riemann sums provide a powerful visual and conceptual framework for understanding the fundamentals of calculus. By breaking down a complex function into simpler components, students can grasp the underlying principles of integration. This step-by-step approach not only aids in mathematical understanding but also fosters critical thinking and problem-solving skills.”
Key Takeaway:
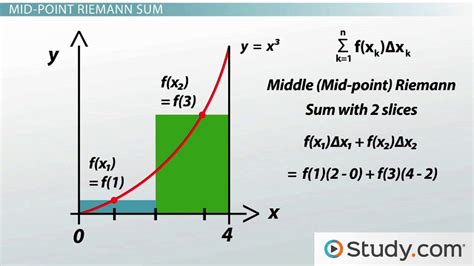
Riemann sums offer a versatile and accessible method to approximate areas under curves, laying the foundation for more advanced calculus concepts. By following these five steps, you can unlock the power of Riemann sums and begin exploring the fascinating world of integral calculus.
Pro-Con Analysis:
| Pros of Riemann Sums | Cons of Riemann Sums |
|---|---|
| Provides an intuitive understanding of integration | May not yield exact results for non-rectangular shapes |
| Can be used for a wide range of functions | Requires careful choice of sample points and sub-intervals |
| Offers a visual representation of the integral | Computationally intensive for complex functions |
| Helps develop problem-solving skills | May not capture all nuances of a function’s behavior |

FAQ Section:
What is the primary purpose of Riemann sums in calculus?
+Riemann sums serve as a fundamental tool in calculus to approximate the area under curves, enabling the evaluation of integrals and the accumulation of quantities over a given interval.
Can Riemann sums be used for all types of functions?
+While Riemann sums can be applied to a wide range of functions, their effectiveness may vary. Functions with discontinuities or sharp turns may require careful choice of sample points and sub-intervals.
How do Riemann sums relate to the fundamental theorem of calculus?
+Riemann sums provide the conceptual foundation for the fundamental theorem of calculus. By taking the limit of Riemann sums as the number of sub-intervals approaches infinity, we arrive at the exact value of the integral.
Are there any alternative methods to Riemann sums for integration?
+Yes, there are alternative methods such as trapezoidal sums, Simpson's rule, and numerical integration techniques. Each method has its strengths and is suitable for different types of functions and scenarios.
By delving into the intricacies of Riemann sums, we’ve uncovered a powerful tool that forms the bedrock of integral calculus. With this guide, we hope to have illuminated the path towards a deeper understanding of this essential mathematical concept.



