How to Convert RPM to Radians
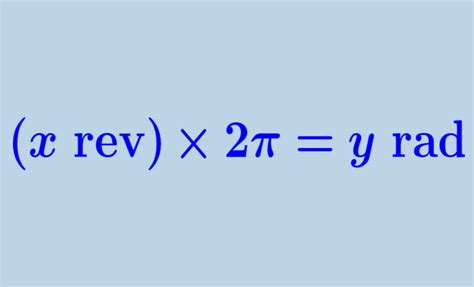
Converting revolutions per minute (RPM) to radians is a fundamental concept in various fields, including engineering, physics, and data analysis. This process is essential for understanding rotational motion and its applications. Let’s dive into the steps and explore some practical examples.
The Conversion Formula: The key to transforming RPM into radians lies in understanding the relationship between these two units of measurement. RPM represents the number of revolutions completed in one minute, while radians measure the angle of rotation. To make this conversion, we utilize a straightforward formula:
\[ \begin{equation*} \text{Radians} = 2\pi \cdot \text{RPM} \cdot \text{time (in minutes)}\,. \end{equation*} \]
Here, 2\pi represents the constant value of approximately 6.28318, which arises from the definition of a radian as the angle subtended by an arc of a circle that is equal in length to the radius.
Step-by-Step Conversion Process:
Identify the RPM Value: Start by determining the RPM you wish to convert. This value represents the number of revolutions per minute and is typically provided in mechanical or engineering contexts.
Determine the Time Interval: Next, consider the time interval for which the RPM value is given. This could be a single minute, multiple minutes, or even fractions of a minute.
Apply the Formula: Use the conversion formula to calculate the corresponding angle in radians. Simply multiply the RPM value by 2\pi and then by the time interval (in minutes).
Express the Result: The final answer will be the angle of rotation in radians. This value represents the angular displacement or the amount of rotation that has occurred during the given time interval.
Real-World Application: Imagine you’re analyzing the performance of a wind turbine. The turbine’s blades rotate at a constant speed of 20 RPM. To understand the angular displacement of the blades over a 5-minute period, you would calculate:
\[ \begin{align*} \text{Radians} &= 2\pi \cdot 20 \text{ RPM} \cdot 5 \text{ minutes} \\ &= 628.318 \text{ radians}\,. \end{align*} \]
This means that over a 5-minute period, the wind turbine’s blades would have rotated through an angle of approximately 628.318 radians.
Practical Tips: - When dealing with fractional RPM values, ensure you maintain precision in your calculations to avoid rounding errors. - Remember that the conversion from RPM to radians is a one-to-one relationship; each revolution corresponds to 2\pi radians. - For complex mechanical systems, this conversion is crucial for analyzing and optimizing performance, especially when dealing with gear ratios or angular velocity calculations.
Key Takeaway: Converting RPM to radians is a fundamental skill for engineers and scientists working with rotational motion. By understanding and applying this conversion, professionals can accurately analyze and design systems involving rotating components.
FAQ:
How does the conversion formula account for the circular nature of rotations?
+The conversion formula incorporates the constant 2\pi to account for the circular nature of rotations. This constant represents the ratio of the circumference of a circle to its radius, ensuring that the conversion accurately represents the angular displacement in radians.
Can RPM be converted directly to degrees, or is radians the only option?
+While radians are the standard unit for angular measurements, RPM can be converted to degrees. The conversion formula for degrees involves multiplying RPM by 360^\circ (the number of degrees in a full circle) and then by the time interval. However, radians are often preferred due to their mathematical simplicity and compatibility with advanced calculations.
Are there any practical scenarios where converting RPM to radians is not necessary?
+In some cases, especially when dealing with basic mechanical systems or everyday applications, converting RPM to radians might not be essential. However, for precise engineering calculations, especially in fields like robotics or aerospace, the conversion is crucial to ensure accurate analysis and design.
How does the conversion from RPM to radians impact the analysis of angular velocity?
+Converting RPM to radians is fundamental for calculating angular velocity, which is typically measured in radians per second. By converting RPM to radians, you can determine the rate of change of angular displacement, allowing for more accurate analysis of rotating systems’ dynamics.



