Multiples and Submultiples: A Quick Guide

Welcome to an essential guide on understanding multiples and submultiples, a fundamental concept in mathematics and various scientific disciplines. In this article, we will delve into the intricacies of these numerical relationships, exploring their definitions, applications, and significance. Whether you are a student, a researcher, or simply curious about the building blocks of our numerical system, this guide will provide you with a comprehensive understanding of multiples and submultiples.

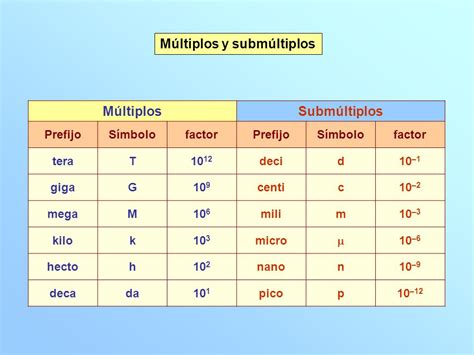
Understanding Multiples and Submultiples

Multiples and submultiples are mathematical concepts that describe the relationship between numbers, forming the basis for understanding quantity, measurement, and scaling. Multiples refer to the products obtained when a given number, known as the base or factor, is multiplied by an integer. On the other hand, submultiples represent the division of the base number by an integer, resulting in smaller parts or fractions.

These concepts are integral to our daily lives, influencing various fields such as physics, engineering, economics, and even music theory. For instance, in music, understanding multiples helps us grasp concepts like octave intervals and harmonics, while submultiples are essential for understanding fractions of notes and the division of time signatures.

Defining Multiples

A multiple of a number x is any product obtained by multiplying x by an integer. For example, if we consider the number 5, its multiples include 5, 10, 15, 20, and so on. In this case, the integer used for multiplication can be 1, 2, 3, or any other positive integer.

Mathematically, we can represent multiples as follows: x * n, where x is the base number and n is the integer multiplier. So, the multiples of 5 can be written as 5 * 1, 5 * 2, 5 * 3, and so forth.

Exploring Submultiples

Submultiples, also known as divisors, are the results of dividing the base number by an integer. For instance, the submultiples of 10 include 1, 2, 5, and 10, as these are the values obtained when dividing 10 by 1, 2, 5, or 10, respectively. It’s important to note that the divisor, or the integer used for division, must be a positive integer greater than zero.

In mathematical notation, submultiples can be represented as x / n, where x is the base number and n is the integer divisor. For example, the submultiples of 12 can be expressed as 12 / 1, 12 / 2, 12 / 3, and so on.

Properties and Applications

Multiples and submultiples possess several interesting properties that make them invaluable in various mathematical and scientific contexts. Understanding these properties allows us to manipulate and analyze numerical data more effectively.

Common Multiples and Least Common Multiple (LCM)

When dealing with multiples of different numbers, we often encounter common multiples, which are the products shared by two or more numbers. For instance, the common multiples of 3 and 4 include 12, 24, and 36. These common multiples can be useful for understanding relationships between quantities or for finding the least common multiple (LCM), which is the smallest multiple shared by two or more numbers.

The LCM is particularly important in fields like engineering, where it helps determine the compatibility of different components or systems. For example, in electrical engineering, the LCM of the frequencies of two signals can be used to find the least common interval at which both signals can be sampled simultaneously.

Highest Common Factor (HCF) and Prime Factorization

Submultiples also play a crucial role in understanding the highest common factor (HCF) of two or more numbers. The HCF, also known as the greatest common divisor (GCD), is the largest submultiple shared by a set of numbers. For instance, the HCF of 18 and 30 is 6, as it is the largest number that divides both 18 and 30 exactly.

The concept of HCF is closely related to prime factorization, which is the process of expressing a number as a product of prime factors. Prime factors are numbers that can only be divided by 1 and themselves. For example, the prime factorization of 24 is 2 * 2 * 2 * 3, which simplifies to 2^3 * 3.

Prime factorization is a powerful tool in number theory and has numerous applications in cryptography, data compression, and error-correcting codes.

Fractions and Decimal Representations

Submultiples are essential for understanding fractions and decimal representations. When we divide a number by an integer, we obtain a fraction, which represents a part of the whole. For instance, dividing 10 by 2 gives us the fraction ¹⁰⁄₂, which is equivalent to the decimal 5.0. Similarly, dividing 25 by 5 results in the fraction ²⁵⁄₅, which simplifies to 5, or the decimal 5.0.

Fractions and decimals are ubiquitous in scientific and engineering applications, where they are used to represent precise measurements, probabilities, and proportions.

Scaling and Proportionality

Multiples and submultiples are fundamental to the concept of scaling and proportionality. Scaling involves changing the size or magnitude of an object or quantity while maintaining its proportional relationships. For example, when we scale a drawing to twice its original size, we are essentially multiplying each dimension by a factor of 2.

In fields like physics and chemistry, scaling is essential for understanding phenomena at different scales, such as the behavior of atoms or the motion of celestial bodies. In economics, scaling is crucial for analyzing the impact of changes in one variable on another, such as the effect of population growth on resource consumption.

Real-World Examples and Applications

The concepts of multiples and submultiples are deeply ingrained in our daily lives and various scientific disciplines. Let’s explore some real-world examples and applications to understand their significance.

Time and Frequency

In the domain of time, multiples and submultiples are used to define units of measurement. For instance, a minute is a multiple of 60 seconds, and an hour is a multiple of 60 minutes. Similarly, in the context of frequency, multiples and submultiples are used to describe the relationship between different frequencies. For example, the frequency of a musical note an octave higher is double the original frequency.

Length and Distance

When measuring length and distance, multiples and submultiples are essential for converting between different units. For example, converting kilometers to meters involves multiplying by 1000, as there are 1000 meters in a kilometer. Similarly, converting inches to centimeters requires multiplying by 2.54, as there are approximately 2.54 centimeters in an inch.

Money and Economics

In economics and finance, multiples and submultiples are used to analyze and compare different financial metrics. For instance, the price-earnings ratio (P/E ratio) is a multiple that relates a company’s stock price to its earnings per share. A higher P/E ratio indicates that investors are willing to pay more for each unit of earnings, suggesting a higher valuation for the company.

Computer Science and Information Technology

In the digital world, multiples and submultiples are crucial for understanding data storage, transmission, and processing. For example, the storage capacity of a hard drive is often expressed in multiples of gigabytes (GB), with each GB representing 1,000,000,000 bytes. Similarly, network speeds are often measured in multiples of bits per second (bps), with common values including kilobits per second (Kbps), megabits per second (Mbps), and gigabits per second (Gbps).

Conclusion: The Significance of Multiples and Submultiples

Multiples and submultiples are fundamental concepts that underpin our understanding of numbers, quantities, and relationships. They are ubiquitous in various fields, from music and art to physics and engineering, economics, and computer science. By grasping these concepts, we can better comprehend the world around us and solve complex problems more effectively.

This guide has provided an overview of multiples and submultiples, their definitions, properties, and real-world applications. By exploring these concepts in depth, we hope to have illuminated their significance and inspired further exploration and understanding.