The Ultimate Guide to Pythagorean Theorem

Step into the world of mathematics, where the ancient wisdom of Pythagoras continues to shape our understanding of geometry and the very fabric of our universe. The Pythagorean Theorem, a cornerstone of mathematics, has captivated scholars and students alike for centuries. Its simplicity belies its profound impact on our comprehension of shapes, distances, and the underlying order of the world. In this comprehensive guide, we’ll delve deep into the heart of this theorem, exploring its history, applications, and enduring relevance in modern times.

Historical Roots: Unraveling the Ancient Mystery

The origins of the Pythagorean Theorem can be traced back to ancient Greece, specifically to the enigmatic figure of Pythagoras, a mathematician and philosopher who lived in the 6th century BCE. Pythagoras, often regarded as the first pure mathematician, left an indelible mark on the world of mathematics. The theorem that bears his name is a testament to his genius and the enduring legacy of ancient Greek mathematical thought.

However, the story of this theorem doesn’t begin and end with Pythagoras. In fact, the concept of the theorem can be found in ancient texts from across the globe, suggesting that multiple civilizations independently discovered this fundamental principle. From the Babylonians to the ancient Chinese, the understanding of right-angled triangles and their unique properties has been a universal mathematical insight.

A Theorem’s Definition: Breaking It Down

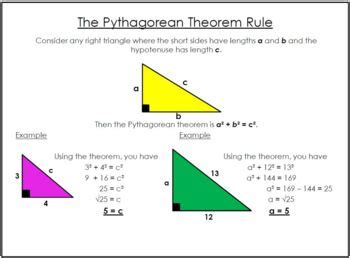
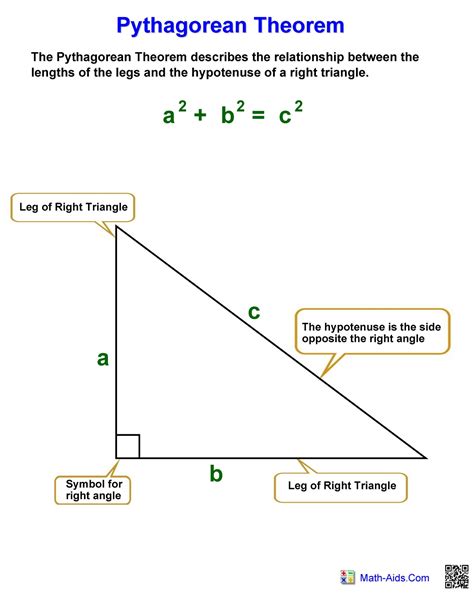
At its core, the Pythagorean Theorem is a mathematical relationship between the sides of a right-angled triangle. This theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides. Mathematically, this can be expressed as:

c² = a² + b²

Where: - c is the length of the hypotenuse - a and b are the lengths of the other two sides

This simple equation encapsulates a profound truth about the nature of triangles and the geometric relationships that underpin our understanding of space and distance.

Practical Applications: The Theorem in Action

The Pythagorean Theorem is more than just a theoretical concept; it has practical applications that are integral to various fields and everyday life. Here are some key areas where this theorem comes into play:

• Engineering and Construction: Builders and engineers use the theorem to calculate distances, plan structures, and ensure the stability of various designs. From determining the length of roof beams to calculating the height of a building, the theorem is a fundamental tool.

• Navigation and Mapping: In the realm of geography and navigation, the theorem is invaluable. It helps in calculating distances between two points, particularly in the context of air and sea travel, where accurate distance measurement is crucial.

• Physics and Mechanics: The theorem finds application in physics, especially in the study of motion and forces. It aids in understanding the relationships between different forces acting on an object, and in calculating the energy associated with those forces.

• Computer Graphics and Gaming: In the digital world, the theorem is used to create realistic graphics and animations. It helps in calculating the positions and movements of objects within a virtual space, ensuring that the visual representations are accurate and true to life.

Visualizing the Theorem: A Journey Through Triangles

To truly grasp the Pythagorean Theorem, it’s essential to visualize the concept in action. Let’s take a look at a simple example:

Imagine a right triangle with sides of lengths 3 units (side a), 4 units (side b), and an unknown length for the hypotenuse (side c). Applying the Pythagorean Theorem, we can calculate the length of the hypotenuse:

c² = 3² + 4² c² = 9 + 16 c² = 25 c = 5

So, the length of the hypotenuse is 5 units. This simple calculation showcases the power of the theorem, allowing us to determine unknown distances and relationships within a triangle.

Myth vs. Reality: Dispelling Common Misconceptions

Despite its widespread use and understanding, the Pythagorean Theorem is not without its myths and misconceptions. Here, we address some common misconceptions and provide clarity:

• The Theorem Only Applies to Right Triangles: While the theorem is primarily associated with right triangles, its principles can be extended to other shapes and mathematical concepts. The theorem’s underlying principles of distance and relationship can be applied to various geometric figures.

• The Theorem is Infallible: While the theorem is a fundamental truth in mathematics, it is not without its limitations. In certain non-Euclidean geometries, the theorem may not hold true. Understanding these exceptions is crucial to a comprehensive grasp of the theorem’s scope.

• The Theorem is Only for Advanced Mathematicians: On the contrary, the Pythagorean Theorem is a fundamental concept that forms the basis of geometric understanding. It is accessible to students of all ages and can be a gateway to more advanced mathematical concepts.

A Global Perspective: The Theorem’s Reach

The Pythagorean Theorem’s impact is not confined to any one region or culture. Its principles have been adopted and built upon by mathematicians worldwide, leading to advancements in various fields. From ancient Indian mathematicians who used the theorem in their astronomical calculations to modern-day researchers who apply it in quantum physics, the theorem’s reach is truly global.

Looking Ahead: Future Applications and Trends

As we continue to explore the frontiers of mathematics and science, the Pythagorean Theorem remains a cornerstone of our understanding. Its applications are expected to grow, especially in the field of data science and artificial intelligence. The theorem’s ability to provide precise calculations and relationships makes it an invaluable tool for analyzing complex data sets and predicting outcomes.

In conclusion, the Pythagorean Theorem is more than just a mathematical formula; it is a gateway to understanding the underlying order of our universe. Its applications are vast, and its impact is felt across various disciplines. As we continue to explore the depths of mathematics, the legacy of Pythagoras and his theorem will undoubtedly continue to guide and inspire.