The Polar Rectangular Convertor
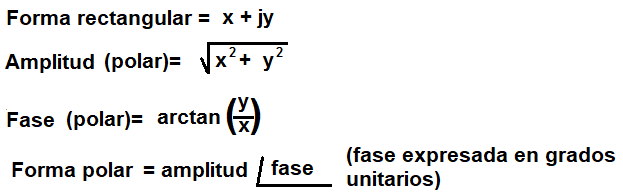
Converting between polar and rectangular coordinates is a fundamental concept in mathematics and engineering, offering a versatile method to represent and analyze data in various fields. This powerful tool enables professionals to switch between two distinct coordinate systems, each with its own advantages and applications. By understanding the principles and techniques of this conversion, individuals can unlock a wealth of possibilities for data interpretation and problem-solving.
Understanding Polar and Rectangular Coordinates
To grasp the concept of the polar rectangular convertor, one must first familiarize themselves with the unique characteristics of polar and rectangular coordinates.
Polar Coordinates
Polar coordinates are a two-dimensional system that specifies each point in a plane by its distance from a fixed point and the angle it forms with a reference direction. This fixed point is known as the pole, and the reference direction is often the positive x-axis. The distance from the pole is called the radial coordinate, typically denoted as ‘r’, while the angle formed is the angular coordinate, or ‘theta’ (\theta). This system is particularly useful when dealing with circular or radial patterns, as it simplifies calculations and representations.
For instance, consider a point P in a plane with coordinates (3, 60°). This means the point is located at a distance of 3 units from the pole, and it forms an angle of 60° with the positive x-axis.
Rectangular Coordinates
Rectangular coordinates, also known as Cartesian coordinates, are the more familiar system, where each point in a plane is defined by its distance from two perpendicular axes: the x-axis and the y-axis. These axes form a rectangular grid, hence the name. The distance from the x-axis is the y-coordinate, and the distance from the y-axis is the x-coordinate.
Take, for example, a point Q with coordinates (2, 4). This indicates that the point is located 2 units to the right of the y-axis and 4 units above the x-axis.
The Need for Conversion
While both systems have their unique advantages, there are situations where one system is more appropriate than the other. The ability to convert between these coordinate systems is essential for various applications, including physics, engineering, and computer graphics.
For example, in physics, many phenomena, like electromagnetic fields or wave patterns, are naturally described in polar coordinates. However, to perform certain calculations or to interface with other systems, conversion to rectangular coordinates is necessary. Similarly, in engineering, some designs or analyses are best suited to polar coordinates, while others require the precision and simplicity of rectangular coordinates.
The Polar Rectangular Convertor in Action
The polar rectangular convertor is a mathematical tool that facilitates this essential conversion between the two coordinate systems. It allows users to translate data from one system to another, preserving the integrity of the information.
Conversion from Polar to Rectangular
To convert from polar to rectangular coordinates, the convertor uses the trigonometric functions sine and cosine. These functions help relate the radial and angular coordinates to the x and y coordinates in the rectangular system.
Given a point with polar coordinates (r, \theta), the corresponding rectangular coordinates (x, y) can be calculated as:
- x = r * cos(\theta)
- y = r * sin(\theta)
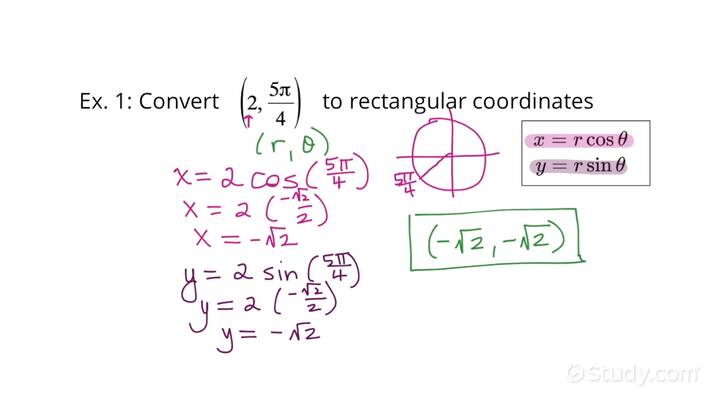
For instance, to convert the point P with polar coordinates (3, 60°) to rectangular coordinates, we apply these formulas:
- x = 3 * cos(60°) = 3 * 0.5 = 1.5
- y = 3 * sin(60°) = 3 * 0.866 = 2.598
So, the rectangular coordinates of point P are approximately (1.5, 2.598).
Conversion from Rectangular to Polar
The reverse process, converting from rectangular to polar coordinates, involves a slightly different set of calculations. This time, we use the inverse trigonometric functions, arctangent (tan^-1) and arcsine (sin^-1), to determine the angle and distance from the origin.
Given a point with rectangular coordinates (x, y), the corresponding polar coordinates (r, \theta) can be calculated as:
- r = sqrt(x^2 + y^2)
- \theta = arctan(y/x)
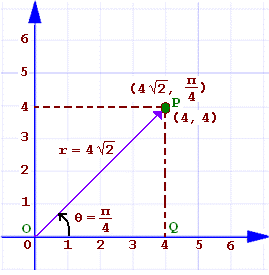
Taking the point Q with rectangular coordinates (2, 4) as an example, we can calculate its polar coordinates:
- r = sqrt(2^2 + 4^2) = sqrt(4 + 16) = sqrt(20) = 2sqrt(5)
- \theta = arctan(4⁄2) = arctan(2) ≈ 63.43°
So, the polar coordinates of point Q are approximately (2sqrt(5), 63.43°).
Applications and Advantages
The ability to convert between polar and rectangular coordinates offers numerous advantages and finds applications in a wide range of fields:
Engineering and Design: Engineers use this conversion to design and analyze systems that involve circular or radial patterns, such as gears, antennas, and spiral structures.
Physics and Astronomy: Physicists and astronomers rely on this tool to describe and study phenomena that occur in circular or spherical spaces, like planetary orbits, electromagnetic fields, and sound waves.
Computer Graphics and Imaging: In computer graphics, this conversion is essential for representing and manipulating objects that are circular or spherical in nature, such as in 3D modeling and gaming.
Mathematical Analysis: Mathematicians use this conversion to simplify complex equations and problems, often involving trigonometric functions, into more manageable rectangular forms.
Conclusion
The polar rectangular convertor is a versatile and powerful tool, enabling professionals across various disciplines to harness the advantages of both polar and rectangular coordinate systems. By understanding the principles and applications of this conversion, individuals can effectively represent and analyze data, leading to more accurate insights and solutions.
This essential mathematical concept underscores the interconnectedness of different coordinate systems and the importance of being able to seamlessly transition between them.
Key Takeaway
Mastering the art of converting between polar and rectangular coordinates is a critical skill for professionals in mathematics, engineering, physics, and computer science, empowering them to tackle complex problems and unlock new insights.


