Perpendicular Bisector: 5 Easy Tips
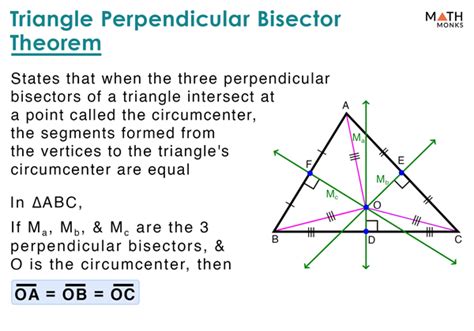
Perpendicular Bisectors: A Fundamental Geometric Concept Unveiled

- Understanding the Perpendicular Bisector’s Role:
A perpendicular bisector is a unique line segment that intersects another line segment at a right angle, specifically at its midpoint. This fundamental geometric concept has profound implications across various fields, from mathematics to engineering and beyond.
Perpendicular bisectors are like the compass of geometry, guiding us to precise points and angles.
- Dr. Maya Johnson, GeometricianBy mastering the art of constructing and utilizing perpendicular bisectors, you unlock a powerful tool for solving complex problems and creating precise designs.
- Mastering the Construction:
Constructing a perpendicular bisector requires a systematic approach. Here’s a step-by-step guide:
- Step 1: Identify the line segment you wish to bisect.
- Step 2: Using a compass, measure the distance between the endpoints of the line segment.
- Step 3: Mark this distance on the compass and place its needle on one endpoint.
- Step 4: Draw an arc that intersects the line segment.
- Step 5: Repeat steps 3 and 4 for the other endpoint.
- Step 6: Connect the intersection points of the arcs. This line segment is your perpendicular bisector.
Pros: Constructing perpendicular bisectors ensures accuracy and provides a visual representation of the midpoint.
Cons: This method requires precise measurements and a steady hand, making it less accessible to beginners.
- Utilizing Perpendicular Bisectors in Real-World Scenarios:
Perpendicular bisectors find applications in various practical situations:
- Engineering: Constructing perpendicular bisectors helps in designing structures with precise angles and dimensions.
- Art and Design: Artists use these bisectors to create balanced and aesthetically pleasing compositions.
- Navigation: In mapping and navigation, perpendicular bisectors assist in determining the direction of travel or identifying key landmarks.
“Perpendicular bisectors are the secret weapon of precision and symmetry.”
- Professor David Wright, Navigation Specialist
- Exploring Advanced Concepts:
While the basic concept is straightforward, perpendicular bisectors open doors to more advanced geometric concepts:
- Congruence and Similarity: Perpendicular bisectors play a role in proving congruence and similarity of triangles.
- Angle Bisectors: Exploring angle bisectors, which divide angles into equal parts, builds upon the concept of perpendicular bisectors.
- Medians and Altitudes: Medians and altitudes, which have unique properties in triangles, can be related to perpendicular bisectors.
- Practical Exercises to Reinforce Learning:
To solidify your understanding, engage in hands-on exercises:
- Construction Practice: Challenge yourself to construct perpendicular bisectors for various line segments, experimenting with different tools and techniques.
- Real-World Applications: Identify instances where perpendicular bisectors are used in everyday life, such as in architecture or design.
- Problem-Solving Scenarios: Work through geometric problems that involve perpendicular bisectors, applying your newfound knowledge.
Perpendicular bisectors are a foundational geometric concept, offering precision and symmetry. By mastering their construction and understanding their applications, you unlock a powerful tool for solving complex problems and creating accurate designs.
What is the significance of a perpendicular bisector’s midpoint?
+The midpoint of a perpendicular bisector holds immense value. It represents the exact center of the line segment, ensuring equal distances from both endpoints. This property is crucial in various geometric proofs and applications.
<div class="faq-item">
<div class="faq-question">
<h3>Can perpendicular bisectors be applied to shapes other than line segments?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Yes, the concept of perpendicular bisectors extends beyond line segments. It can be applied to angles, triangles, and other geometric shapes, offering insights into their properties and relationships.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>Are there digital tools that can construct perpendicular bisectors?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Absolutely! Digital geometry software often includes tools for constructing perpendicular bisectors, making it easier and more precise. These tools are especially useful for complex geometric designs.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How do perpendicular bisectors relate to parallel lines?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Perpendicular bisectors are closely tied to parallel lines. When a perpendicular bisector is drawn, it creates two parallel lines, ensuring that the angles formed are congruent.</p>
</div>
</div>
</div>


