Mastering One-Factor ANOVA Analysis
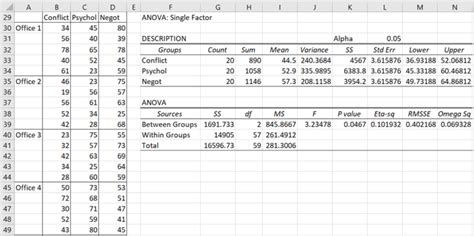
Welcome to a comprehensive guide on mastering the art of One-Factor ANOVA analysis, a powerful statistical tool used to compare and analyze the means of different groups. This article will delve deep into the intricacies of ANOVA, providing you with a solid understanding of its concepts and practical applications. By the end of this journey, you'll be equipped with the knowledge to confidently conduct and interpret One-Factor ANOVA analyses, unlocking a world of insights from your data.
Understanding One-Factor ANOVA: A Comprehensive Overview

Analysis of Variance, or ANOVA, is a statistical method used to compare and analyze the means of three or more groups. It's a powerful tool that allows researchers, scientists, and data analysts to make informed decisions based on data-driven evidence. The One-Factor ANOVA, also known as One-Way ANOVA, is a specific type of ANOVA where there's a single independent variable with multiple levels or categories.
Imagine you're a market researcher studying the effectiveness of different advertising campaigns. You've designed three unique campaigns and want to know which one performs the best. Here's where One-Factor ANOVA steps in. It enables you to analyze the data from each campaign, compare the means, and determine if there's a statistically significant difference between them.
The Key Components of One-Factor ANOVA
One-Factor ANOVA primarily focuses on a single independent variable, often referred to as the factor or treatment. This factor has two or more levels, representing the different groups or conditions you're comparing. For instance, in our advertising campaign example, the factor could be the "Campaign Type" with levels such as "Campaign A", "Campaign B", and "Campaign C".
The dependent variable, on the other hand, is the outcome or response you're interested in measuring. In our case, this could be the "Number of Sales" or "Customer Engagement" generated by each campaign.
One-Factor ANOVA aims to answer a crucial question: "Are the means of the dependent variable significantly different across the levels of the independent variable?" If the answer is yes, it indicates that at least one of the groups has a mean that's statistically different from the others.
How ANOVA Works: A Simplified Explanation
ANOVA operates by comparing the variance between groups to the variance within groups. It calculates the F-statistic, which is the ratio of these two variances. If the F-statistic is large enough, it suggests that the variances are significantly different, leading to the rejection of the null hypothesis. This means there's likely a real difference in the means of the groups.
The null hypothesis (H0) states that all group means are equal, while the alternative hypothesis (Ha or H1) claims that at least one group mean is different. By comparing the calculated F-statistic to a critical value from an F-distribution, we can determine if there's enough evidence to reject the null hypothesis.
| Factor | Levels |
|---|---|
| Campaign Type | Campaign A, Campaign B, Campaign C |
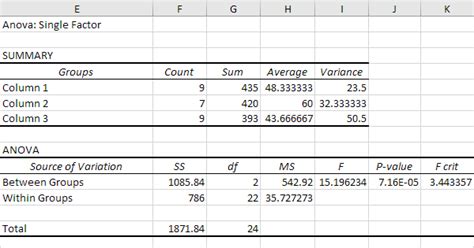
Conducting One-Factor ANOVA: A Step-by-Step Guide

Now, let's dive into the practical side of One-Factor ANOVA. We'll walk through the steps to conduct an ANOVA analysis, using a real-world example to bring the process to life.
Step 1: Data Collection and Preparation
The first step in any statistical analysis is to collect your data. In our advertising campaign example, you'd need to gather data on the sales or engagement generated by each campaign. This data should be representative of the population you're interested in studying.
Once you have your data, it's essential to ensure it's clean and ready for analysis. This involves checking for any missing values, outliers, or errors. You might need to transform or standardize your data to meet the assumptions of ANOVA.
Step 2: Define Your Hypotheses
Before diving into the analysis, it's crucial to define your hypotheses. As mentioned earlier, the null hypothesis (H0) states that there's no significant difference between the means of the groups. The alternative hypothesis (Ha or H1) suggests that at least one group mean is different.
For instance, in our advertising campaign example, the null hypothesis could be: "There's no significant difference in the number of sales generated by the three campaigns." The alternative hypothesis would be: "At least one of the campaigns generates a significantly different number of sales."
Step 3: Check Assumptions
One-Factor ANOVA relies on several assumptions to ensure the validity of its results. These include normality of the data, homogeneity of variances across groups, and the independence of observations. You can use statistical tests like the Shapiro-Wilk test for normality and the Levene's test for homogeneity of variances.
If your data doesn't meet these assumptions, you might need to transform your variables or use alternative analysis methods. It's crucial to ensure the assumptions are met to maintain the reliability of your analysis.
Step 4: Calculate the F-statistic
Once your data is prepared and assumptions are checked, it's time to calculate the F-statistic. This involves computing the between-groups variance (variance due to the effect of the independent variable) and the within-groups variance (variance due to random errors or noise). The F-statistic is then calculated as the ratio of these two variances.
The formula for the F-statistic is:
F-statistic = (Between-groups variance) / (Within-groups variance)
Step 5: Compare to Critical Value
After calculating the F-statistic, you need to compare it to a critical value from an F-distribution. The critical value is determined based on the desired significance level (often 0.05) and the degrees of freedom for the between-groups and within-groups variances.
If the calculated F-statistic is greater than the critical value, it suggests that there's a significant difference between the means of the groups. In this case, you'd reject the null hypothesis and accept the alternative hypothesis.
Step 6: Post-hoc Tests
If you find a significant difference in the means, it's essential to conduct post-hoc tests to determine which specific groups are significantly different from each other. Common post-hoc tests include the Tukey-Kramer test and the Bonferroni test. These tests help pinpoint the specific groups that differ significantly.
Step 7: Interpret and Report Results
Finally, it's time to interpret and report your findings. Provide a clear and concise summary of your results, including the F-statistic, p-value, and any post-hoc test results. Discuss the implications of your findings and how they contribute to your understanding of the problem at hand.
Remember, the interpretation of ANOVA results should be done in the context of your specific research question or problem. It's essential to avoid over-interpreting the results and ensure they align with your initial hypotheses.
| Test | Purpose |
|---|---|
| Shapiro-Wilk | Test for normality of data |
| Levene's | Test for homogeneity of variances |
| Tukey-Kramer | Post-hoc test for comparing group means |
| Bonferroni | Post-hoc test for multiple comparisons |
Advanced Topics in One-Factor ANOVA
While the core concepts of One-Factor ANOVA are essential, there are several advanced topics that can enhance your understanding and skills in this area. These topics delve deeper into the intricacies of ANOVA and provide valuable insights for more complex analyses.
Repeated Measures ANOVA
In some cases, you might be interested in comparing the means of multiple groups, but the data is collected from the same subjects or samples. This is where Repeated Measures ANOVA comes into play. It's used when the same subjects are measured repeatedly under different conditions or at different times.
For example, imagine you're a psychologist studying the effects of different therapy techniques on patients. You measure the patients' stress levels before and after each therapy session. In this case, you'd use Repeated Measures ANOVA to compare the stress levels across the different therapy techniques.
Factorial ANOVA
Factorial ANOVA is a powerful extension of One-Factor ANOVA. It allows you to analyze the effects of two or more independent variables on a single dependent variable. This is particularly useful when you want to study the interaction effects between variables.
Consider a study on the effectiveness of different teaching methods (factor 1) and the use of technology (factor 2) on student performance. Factorial ANOVA would enable you to analyze the main effects of each factor as well as the interaction effect between them.
ANOVA with Transformed Data
Sometimes, your data might not meet the assumptions of ANOVA, such as normality or homogeneity of variances. In such cases, you can apply transformations to your data to make it more suitable for ANOVA analysis. Common transformations include logarithmic, square root, and reciprocal transformations.
For instance, if your data is highly skewed, you might apply a logarithmic transformation to make it more normally distributed.
Multiple Comparisons and Post-hoc Tests
When you find a significant difference in the means using ANOVA, it's essential to conduct post-hoc tests to identify which specific groups are significantly different from each other. These tests help you understand the nature of the differences and provide more detailed insights.
Some common post-hoc tests include the Tukey-Kramer test, the Bonferroni test, and the Dunnett's test. Each of these tests has its own advantages and is used in different scenarios.
Power Analysis and Sample Size Determination
Power analysis is a crucial step in designing your study or experiment. It helps you determine the sample size required to detect a significant effect. By conducting a power analysis, you can ensure that your study has sufficient statistical power to detect meaningful differences.
Several software tools and online calculators can assist you in performing power analysis for One-Factor ANOVA. These tools take into account factors such as the desired power level, effect size, and number of groups.
| Advanced Topic | Description |
|---|---|
| Repeated Measures ANOVA | Used when data is collected from the same subjects under different conditions |
| Factorial ANOVA | Analyzes the effects of multiple independent variables on a single dependent variable |
| Transformed Data | Applying transformations to data that doesn't meet ANOVA assumptions |
| Post-hoc Tests | Tests to identify specific group differences after finding a significant effect in ANOVA |
| Power Analysis | Determining the sample size required to achieve a desired level of statistical power |
Real-World Applications of One-Factor ANOVA
One-Factor ANOVA is a versatile tool with a wide range of applications across various fields. Its ability to compare means and detect significant differences makes it invaluable in research, quality control, and decision-making processes.
Medical Research
In medical research, One-Factor ANOVA is used to compare the effectiveness of different treatments or medications. For instance, a study might compare the recovery rates of patients receiving three different types of surgery for a specific condition.
Marketing and Consumer Research
Marketers often use One-Factor ANOVA to analyze the effectiveness of different marketing strategies or product designs. They might compare the sales or customer feedback for various product variations to determine the most successful approach.
Psychological Studies
Psychologists and behavioral scientists employ One-Factor ANOVA to study the effects of different variables on human behavior. For example, they might compare the performance of students under different teaching methods to identify the most effective approach.
Quality Control in Manufacturing
Manufacturers use One-Factor ANOVA to ensure the quality and consistency of their products. They might compare the performance of different production processes or materials to identify any significant differences in quality.
Social Sciences Research
In the social sciences, One-Factor ANOVA is used to analyze the impact of various factors on human behavior and society. Researchers might compare the opinions or behaviors of people from different demographic groups to understand social trends.
| Field | Application |
|---|---|
| Medical Research | Comparing treatment effectiveness |
| Marketing | Analyzing marketing strategies |
| Psychology | Studying the effects of variables on behavior |
| Manufacturing | Ensuring product quality and consistency |
| Social Sciences | Understanding social trends and behaviors |
FAQs: One-Factor ANOVA

What are the assumptions of One-Factor ANOVA, and how do I check them?
+One-Factor ANOVA relies on several assumptions, including normality of data, homogeneity of variances, and independence of observations. You can use tests like the Shapiro-Wilk test for normality and Levene’s test for homogeneity of variances. If these assumptions aren’t met, you might need to transform your data or use alternative methods.
How do I choose the appropriate post-hoc test after finding a significant effect in ANOVA?
+The choice of post-hoc test depends on the nature of your data and the specific research question. Common post-hoc tests include the Tukey-Kramer test, the Bonferroni test, and the Dunnett’s test. Each test has its own advantages and is used in different scenarios. Consider factors like sample



