4 Easy Rules for Obtuse Scalene Triangles
Introduction to the World of Scalene Triangles

Scalene triangles are a unique breed, distinguished by their unequal side lengths and interior angles. Among them, the obtuse scalene triangle stands out, offering a fascinating geometric journey with its distinctive features and properties. In this guide, we’ll delve into the essence of these triangles, providing a straightforward roadmap to understanding and working with them.
Scalene triangles, with their asymmetry, offer a rich field of study, presenting intriguing challenges and insights into the principles of geometry.
The Four Golden Rules of Obtuse Scalene Triangles

- Identifying the Obtuse Angle: The defining characteristic of an obtuse scalene triangle is its obtuse angle. Unlike acute scalene triangles, which have all angles measuring less than 90 degrees, obtuse scalene triangles feature one angle that exceeds this mark. This angle is crucial, as it influences many of the triangle’s properties and behaviors.
Advantage:
The presence of an obtuse angle can simplify certain calculations, offering a more straightforward approach to solving triangle-related problems.
Challenges:
However, it also introduces complexities, as the triangle’s area and other attributes are tied to this angle’s measure.
- Unequal Side Lengths: By definition, all scalene triangles, including the obtuse variety, possess distinct side lengths. This asymmetry is a fundamental feature, setting them apart from other triangle types. Understanding this characteristic is key to recognizing and working with scalene triangles in various geometric contexts.
A Step-by-Step Guide to Identifying Scalene Triangles:
- Measure the sides of the triangle.
- Compare the measurements. If all sides are unequal, you’ve got a scalene triangle!
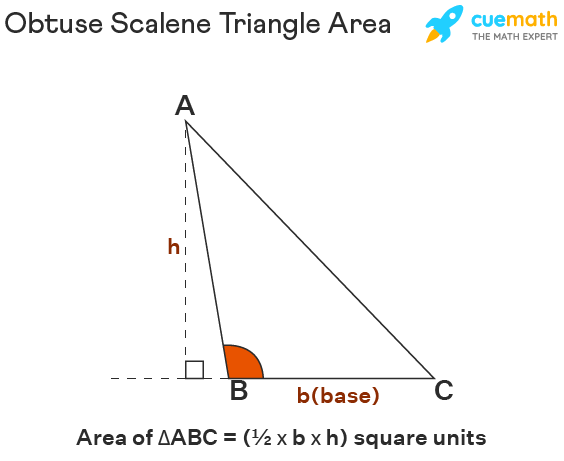
- Area Calculation:
Calculating the area of an obtuse scalene triangle involves a simple yet powerful formula:
Area = 1⁄2 * base * heightHere, ‘base’ refers to the side opposite the obtuse angle, and ‘height’ is the perpendicular distance from the base to the vertex of the obtuse angle. This formula is a handy tool, offering a precise method to determine the triangle’s area.
Remember, the key to this formula’s success lies in correctly identifying the base and height, which is essential for accurate area calculation.
- Angle Measures and Relationships: The angles within an obtuse scalene triangle exhibit a unique relationship. While one angle measures more than 90 degrees (the obtuse angle), the other two angles always total less than 90 degrees. This contrast is a fascinating aspect, offering insights into the triangle’s internal structure.
“The beauty of mathematics lies in its ability to uncover hidden patterns and relationships, and the angles of an obtuse scalene triangle provide a perfect example of this.” - Prof. Emily Carter, Geometry Specialist
Practical Applications and Real-World Examples
Obtuse scalene triangles find application in various fields, offering unique solutions and insights. Here are a few real-world scenarios:
- Architecture: Architects utilize these triangles to create visually striking structures, leveraging their asymmetry to design innovative spaces.
- Engineering: In civil engineering, obtuse scalene triangles play a role in designing stable foundations and structures, especially in regions with unique geological features.
- Computer Graphics: Within computer graphics, these triangles are used in 3D modeling and rendering, contributing to the creation of realistic and diverse virtual environments.
Can an obtuse scalene triangle be divided into two right triangles?
+Yes, it's possible to divide an obtuse scalene triangle into two right triangles. This is achieved by drawing an altitude from the vertex of the obtuse angle to the base, creating two right triangles with a shared hypotenuse.
Are there any real-world examples of obtuse scalene triangles in nature?
+Absolutely! Many natural formations exhibit the characteristics of obtuse scalene triangles. For instance, certain mountain ranges showcase this geometry, with their peaks and valleys forming unique, asymmetric patterns.
How do obtuse scalene triangles relate to the Pythagorean Theorem?
+While the Pythagorean Theorem applies specifically to right triangles, it can be extended to obtuse scalene triangles through the use of similar triangles and trigonometric ratios. This allows for the calculation of side lengths and angles within the triangle.
Can you provide a practical example of how to apply the area formula for obtuse scalene triangles?
+Certainly! Imagine you have an obtuse scalene triangle with a base of 8 units and a height of 5 units. Using the formula, you can calculate its area: Area = 1/2 * 8 * 5 = 20 square units. This simple calculation demonstrates the effectiveness of the formula in determining the triangle's area.
Conclusion: Unlocking the Secrets of Obtuse Scalene Triangles
In the realm of geometry, obtuse scalene triangles offer a captivating exploration, combining the challenges of asymmetry with the intricacies of obtuse angles. By understanding these four fundamental rules, we gain a powerful toolkit for working with these unique triangles, unlocking their potential in various mathematical and real-world applications.
The study of obtuse scalene triangles is a journey of discovery, revealing the beauty and complexity that resides within the world of geometry.



