Uncovering the Secrets of Obtuse-Acute Triangles
In the realm of geometry, triangles hold a unique place, with their distinctive shapes and properties offering a rich field of exploration. Among these, the obtuse-acute triangle stands out as a fascinating subject, combining the characteristics of both obtuse and acute angles to create a distinct mathematical entity. This article delves into the secrets of this triangle, exploring its definition, properties, and the intriguing mathematical landscape it inhabits.
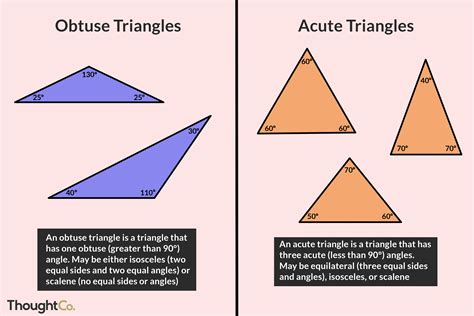
At its core, an obtuse-acute triangle is a three-sided polygon that possesses one obtuse angle (greater than 90 degrees) and two acute angles (less than 90 degrees). This seemingly simple definition belies the complex mathematical relationships and applications that arise from this shape. The unique angle configuration of the obtuse-acute triangle sets it apart from other triangle types, making it a subject of particular interest in various mathematical disciplines.
Historical Evolution: Triangles in Mathematics

To truly understand the significance of the obtuse-acute triangle, it’s essential to explore its historical context within the development of mathematical knowledge. Triangles, as fundamental geometric shapes, have been studied for millennia, with ancient civilizations like the Egyptians and Greeks making significant contributions to our understanding of these figures.
The ancient Greeks, particularly the mathematician Euclid, laid the foundation for much of our modern understanding of triangles. Euclid’s Elements, a seminal work in geometry, included extensive discussions on the properties of triangles, including those with obtuse and acute angles. Through rigorous logical deductions, Euclid established many of the fundamental theorems and principles that govern triangles, providing a solid framework for further exploration.
As mathematical knowledge evolved, so too did the study of triangles. Renaissance mathematicians, such as Leonardo da Vinci and Johannes Kepler, made significant contributions to our understanding of geometric shapes, often drawing inspiration from the natural world. Kepler, for instance, used his knowledge of triangles and their properties to develop his theories on planetary motion, showcasing the practical applications of these geometric principles.
The Unique Properties of Obtuse-Acute Triangles

While all triangles possess certain fundamental properties, the obtuse-acute triangle boasts a set of characteristics that make it distinct from other triangle types.
One notable property is its ability to be classified as both an obtuse and acute triangle simultaneously. This duality arises from the fact that it possesses both an obtuse and acute angle, which sets it apart from other triangle types that fall strictly into one category or the other.
Another intriguing property is the relationship between the lengths of its sides. In an obtuse-acute triangle, the side opposite the obtuse angle is always the longest, while the sides opposite the acute angles are shorter. This property has significant implications for various mathematical calculations and applications, as it provides a clear relationship between the angles and sides of the triangle.
Furthermore, the obtuse-acute triangle has unique properties when it comes to its angles. The sum of the angles in any triangle is always 180 degrees, but in the case of an obtuse-acute triangle, this sum is divided differently among the three angles. The obtuse angle typically accounts for a larger portion of the sum, while the acute angles contribute a smaller share.
Applications in Real-World Scenarios
The obtuse-acute triangle finds application in a variety of real-world scenarios, showcasing its practical utility beyond the realm of pure mathematics.
In architecture and engineering, for instance, the obtuse-acute triangle plays a crucial role in designing structures that require stability and strength. The unique angle configuration of this triangle allows for the distribution of weight and stress in a way that enhances structural integrity. This is particularly evident in the design of bridges, where the obtuse-acute triangle can be found in various components, such as the supports and trusses.
The obtuse-acute triangle also finds application in the field of navigation and surveying. In these disciplines, the principles of trigonometry, which are intimately tied to the properties of triangles, are used to determine distances, angles, and directions. The unique properties of the obtuse-acute triangle, particularly its relationship between angles and sides, make it a valuable tool for calculating distances and angles in various navigation and surveying scenarios.
Myth vs. Reality: Common Misconceptions
Despite its rich mathematical history and practical applications, the obtuse-acute triangle is not without its misconceptions.
One common misconception is that the obtuse-acute triangle is simply a hybrid of an obtuse and acute triangle, created by combining the two. In reality, while it possesses characteristics of both, it is a distinct triangle type in its own right, with unique properties that set it apart from other triangles.
Another misconception is that the obtuse-acute triangle is inherently unstable or weak due to its angle configuration. However, as previously mentioned, the obtuse-acute triangle is often used in architectural and engineering contexts precisely because of its ability to distribute weight and stress effectively, making it a stable and reliable shape for various structural applications.
Conclusion: Unlocking the Secrets

In conclusion, the obtuse-acute triangle is a fascinating mathematical entity, combining the characteristics of both obtuse and acute angles to create a unique shape with distinct properties. Its historical evolution, from ancient civilizations to modern mathematical disciplines, showcases its enduring significance in the field of geometry.
The obtuse-acute triangle’s ability to be classified as both an obtuse and acute triangle simultaneously, its unique relationship between angles and sides, and its practical applications in fields like architecture and navigation, all contribute to its rich mathematical landscape.
By uncovering the secrets of the obtuse-acute triangle, we not only deepen our understanding of this specific triangle type but also gain insights into the broader world of mathematics, where the interplay of shapes, angles, and relationships continues to inspire and challenge our curiosity.
The obtuse-acute triangle, with its unique angle configuration and properties, serves as a testament to the rich and diverse world of mathematics, offering a glimpse into the intricate relationships that govern geometric shapes and their applications.