7 Node Voltage Method Tips

The Node Voltage Method, a fundamental technique in circuit analysis, offers a systematic approach to determining voltage levels at specific points in a circuit. Here’s a detailed guide, enhanced with insights and practical examples, to help you master this method.
Understanding the Basics
The Node Voltage Method is rooted in Kirchhoff’s Current Law (KCL), which states that the current entering a node is equal to the current leaving it. By applying this principle, we can establish a set of equations to solve for the unknown node voltages. These equations represent the balance of currents at each node, providing a powerful tool for circuit analysis.
Step-by-Step Guide to Node Voltage Method:
Identify the Nodes: Start by identifying all the nodes in the circuit. A node is any point where two or more components are connected.
Assign Reference Node: Select one of the nodes as the reference node, typically denoted as node 0 or ground. All other node voltages will be measured relative to this reference.
Apply KCL: For each node, apply Kirchhoff’s Current Law. Write an equation that states the sum of currents entering the node is equal to the sum of currents leaving it. This equation will have one unknown variable, which is the voltage at that particular node.
Determine Branch Currents: Calculate the currents flowing through each branch of the circuit. This can be done using Ohm’s Law ($I = V/R$) or by considering the voltage drop across resistors.
Write Node Equations: For each node, write an equation that represents the balance of currents. The left side of the equation should represent the sum of currents entering the node, while the right side represents the sum of currents leaving.
Solve the System of Equations: The node equations form a system of linear equations. Solve this system to find the values of the unknown node voltages. You can use various methods like Gaussian elimination or matrix inversion.
Check Your Work: After solving, verify your results by checking if the currents entering and leaving each node are indeed equal. This ensures the validity of your calculations.
Tips for Effective Node Voltage Method Application:
Simplify Circuits: Before applying the Node Voltage Method, simplify the circuit by combining resistors in series or parallel wherever possible. This can reduce the number of nodes and equations, making the analysis more manageable.
Use Consistent Sign Conventions: Assign consistent signs to currents and voltages when writing your node equations. For example, currents entering a node could be considered positive, while currents leaving are negative.
Consider Dependent Sources: If your circuit includes dependent sources like voltage-controlled voltage sources or current-controlled current sources, you’ll need to incorporate their relationships into your node equations.
Check for Degeneracy: If you find that some of your node equations are linearly dependent (i.e., they are multiples of each other), you may have a degenerate system of equations. This can happen when you have redundant equations or when your circuit is not fully connected.
Utilize Software: For complex circuits, consider using circuit simulation software that can automate the node voltage analysis. These tools can save time and reduce the risk of errors.
Example Circuit Analysis Using Node Voltage Method:
Let’s apply the Node Voltage Method to a simple circuit:
Circuit Diagram
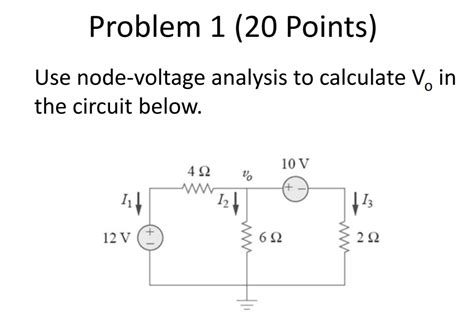
A simple circuit with three nodes: Node 1, Node 2, and Node 3. Node 1 has a 12V voltage source and a 3Ω resistor in series. Node 2 has a 5Ω resistor, and Node 3 has a 4Ω resistor. There is a 2A current source between Node 2 and Node 3.
V1: 12V
R1: 3Ω
R2: 5Ω
R3: 4Ω
I: 2A
Step 1: Identify Nodes
We have three nodes: Node 1, Node 2, and Node 3.
Step 2: Assign Reference Node
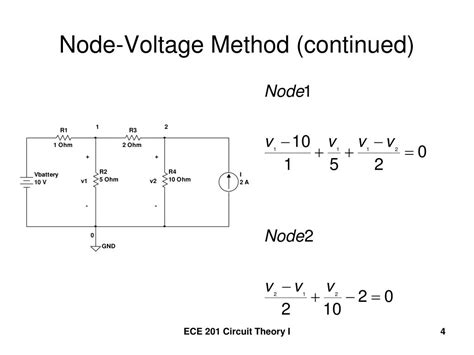
Let's choose Node 3 as our reference node (ground). This means the voltage at Node 3 will be our reference voltage (0V).
Step 3: Apply KCL
For Node 1:
I1 = I2 + I3
where I1 is the current entering Node 1, I2 is the current flowing into Node 2, and I3 is the current flowing into Node 3.
Step 4: Determine Branch Currents

I1 = V1 / R1 = 12V / 3Ω = 4A
I2 = (V2 - V1) / R2 = (unknown - 12V) / 5Ω
I3 = (V3 - V2) / R3 = (unknown - unknown) / 4Ω
Step 5: Write Node Equations
For Node 1: I1 = I2 + I3
4A = (unknown - 12V) / 5Ω + (unknown - unknown) / 4Ω
For Node 2: I2 = I1 + I3
(unknown - 12V) / 5Ω = 4A + (unknown - unknown) / 4Ω
For Node 3: I3 = I2 - I1
(unknown - unknown) / 4Ω = (unknown - 12V) / 5Ω - 4A
Step 6: Solve the System of Equations
Solving the system of equations yields:
V2 = 8V
V3 = 4V
Step 7: Check Your Work
Verifying the currents at each node confirms the accuracy of our calculations.
Common Misconceptions about Node Voltage Method:
Node Voltage vs. Node Current: Node voltage refers to the voltage at a specific node, not the current. While the method is named “Node Voltage Method,” it involves balancing currents at nodes, not voltages.
Number of Equations: The number of equations in the system is equal to the number of nodes, minus one (for the reference node). This is because the reference node voltage is known, so it doesn’t require an equation.
Node Voltage Signs: Node voltages are relative to the reference node. Positive node voltages mean the voltage at that node is higher than the reference node, while negative node voltages indicate a lower voltage.
Future Trends in Node Voltage Method Analysis:
As circuit complexity increases, researchers are exploring advanced techniques to streamline the Node Voltage Method. This includes the development of more efficient algorithms for solving large systems of equations and the integration of machine learning to predict node voltages based on circuit topology.
Conclusion:
Mastering the Node Voltage Method is crucial for circuit analysis, offering a systematic approach to determining node voltages. By following the steps outlined above and understanding the underlying principles, you’ll be well-equipped to tackle a wide range of circuit analysis problems.
Remember, practice is key. The more you apply this method to different circuits, the more intuitive and efficient your analysis will become.



