5 Tips: Negative Integer Subtraction

Mastering the Art of Negative Integer Subtraction: A Comprehensive Guide

Negative integers can be a tricky concept for many, especially when it comes to subtraction. This fundamental mathematical operation often leaves students scratching their heads, wondering how to approach it. But fear not! With a few simple tips and a solid understanding of the rules, negative integer subtraction can become a breeze. Let’s dive in and explore these techniques together.

Tip 1: Understanding the Rules of Negative Integers

Before we tackle subtraction, it’s crucial to grasp the fundamental rules of negative integers. Negative integers are numbers less than zero, and they play a significant role in mathematics. Here’s a quick refresher:

• Negative Numbers and their Properties: Negative integers follow a set of rules that are distinct from positive integers. For instance, when adding two negative numbers, the result is always a negative number. However, subtracting a negative number is where things get interesting.

• Subtracting Negative Numbers: When you subtract a negative number, it’s essentially the same as adding a positive number. In simpler terms, think of it as changing the sign from negative to positive. So, -3 - (-2) is the same as -3 + 2, resulting in -1.

• Absolute Value: Understanding absolute value is key. The absolute value of a negative integer is always positive. For example, |-5| equals 5, indicating that the distance between -5 and zero on the number line is 5 units.

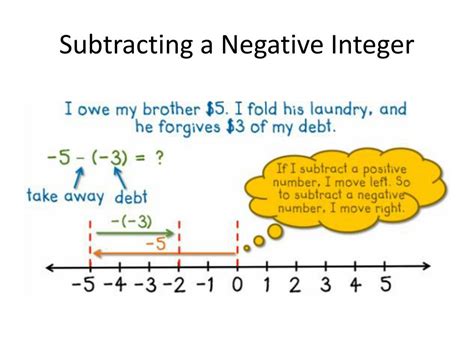
Tip 2: Visualize the Number Line

One effective way to grasp negative integer subtraction is by visualizing it on a number line. This technique provides a concrete representation of the operation, making it easier to comprehend. Here’s how it works:

• Start at the First Number: Begin by placing your finger or a marker at the first number in the subtraction problem. For instance, if you’re solving -5 - (-3), start at -5 on the number line.

• Move Right for Positive Numbers: If the second number is positive, move right on the number line. In our example, since the second number is -3, move three units to the right from -5, landing on -2.

• Move Left for Negative Numbers: If the second number is negative, move left on the number line. For instance, if the problem was -5 - 3, you’d move three units to the left from -5, ending up at -8.

• The Final Position is Your Answer: The number you land on after these movements represents the solution to the subtraction problem.

Tip 3: Think of Subtraction as Addition

A powerful trick to simplify negative integer subtraction is to think of it as addition. This approach might seem counterintuitive, but it can be incredibly helpful. Here’s how it works:

• Change Subtraction to Addition: When faced with a subtraction problem involving negative integers, rewrite it as an addition problem. For example, -5 - (-3) can be rewritten as -5 + 3.

• Add the Numbers: Simply add the numbers together, following the rules of integer addition. In our example, -5 + 3 equals -2.

• Apply the Same Rule for Positive Subtraction: This technique also works for positive subtraction. For instance, 5 - 3 can be rewritten as 5 + (-3), which equals 2.

Tip 4: Practice with Real-World Scenarios

Mathematics is not just about solving abstract problems; it’s about applying these concepts to real-life situations. Here’s a scenario to help you understand negative integer subtraction in a practical context:

Scenario: Imagine you have a savings account with an initial balance of -500. You decide to deposit 300 into the account. How much money will you have in your account after the deposit?

• Solution: Start by rewriting the problem as an addition problem: -500 + 300.

• Add the Numbers: Applying the rules of integer addition, -500 + 300 equals -$200.

• Interpret the Result: After depositing 300, your account balance is now -200, indicating that you still have a negative balance but have reduced it by $300.

Tip 5: Master the Sign Rules

Understanding the rules of signs is essential when working with negative integers. Here’s a quick guide to help you master these rules:

• Adding Negative Numbers: When adding two negative numbers, the result is always negative. For example, -3 + (-2) equals -5.

• Subtracting Negative Numbers: As mentioned earlier, subtracting a negative number is the same as adding a positive number. So, -3 - (-2) is the same as -3 + 2, resulting in -1.

• Mixing Positive and Negative Numbers: When adding or subtracting a mix of positive and negative numbers, pay attention to the signs. For instance, -5 + 3 equals -2, while -5 - 3 equals -8.

• Multiplication and Division: The rules for multiplication and division with negative integers are similar. When multiplying or dividing two negative numbers, the result is positive. For example, (-3) x (-2) equals 6, and (-3) ÷ (-2) equals 1.5.

Conclusion

Negative integer subtraction may seem challenging at first, but with these five tips, you’ll soon become a pro. Remember to understand the rules, visualize the number line, think of subtraction as addition, practice with real-world scenarios, and master the sign rules. With consistent practice and a solid grasp of these concepts, you’ll be able to tackle any negative integer subtraction problem with confidence.