Master the Art: Multiply Binary Numbers in 3 Steps

Step 1: Understand Binary Multiplication Basics
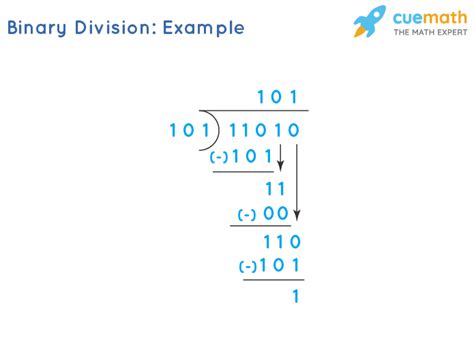
Binary multiplication is a fundamental operation in the world of digital computing and data processing. It’s a process that underpins the very foundation of how computers and electronic devices perform calculations and manipulate information. At its core, binary multiplication involves multiplying two binary numbers, which are represented using only the digits 0 and 1.
In essence, when we multiply binary numbers, we’re essentially performing a series of bitwise AND operations, where each bit of the result is determined by the corresponding bits of the multiplicand and the multiplier. This process is fundamental to understanding how digital systems handle arithmetic operations, which in turn influences the capabilities of computers, smartphones, and other electronic devices.
Step 2: The Process of Binary Multiplication

Binary multiplication can be broken down into a systematic process, which, when followed correctly, yields the correct result. Here’s a step-by-step guide:
- Prepare the Multiplicand and Multiplier. Ensure you have your binary numbers ready. For instance, let's take the example of multiplying the binary number 1011 by 110.
- Set Up the Multiplication Grid. Draw a grid with as many columns as there are digits in the multiplier (in this case, 3) and as many rows as there are digits in the multiplicand (4 in this example). This forms the foundation of your multiplication table.
- Multiply Digit by Digit. Starting with the rightmost digit of the multiplier, multiply it by each digit of the multiplicand. Place the results in the corresponding cells of the grid. For instance, 1 x 110 = 10, so you'd place 0 in the top right cell of the grid, and carry the 1 to the left.
- Repeat for Each Digit. Move left in the multiplier, repeating the multiplication process for each digit. For the next digit, 1 x 110 = 110, so you'd place 0 in the next cell, and carry the 1 to the left again.
- Add the Carried Values. Finally, add up any carried values to the left of each digit to get the final result. In this case, the carried 1s from each multiplication step are added to the leftmost column, giving a final result of 111110.
Step 3: Common Pitfalls and Best Practices
Binary multiplication, while straightforward, can lead to errors if not performed with precision. Here are some tips to ensure accuracy:
Double-Check Your Digits
Always ensure you're multiplying the correct digits together. A single mistake can lead to an incorrect result.Avoid Careless Carrying
Be careful when carrying values over. A misplaced carry can significantly alter your result.Historical Context and Future Trends
Binary multiplication has a rich history in the development of digital technology. Its importance is only expected to grow as we move towards an increasingly digital world. With the rise of quantum computing, binary multiplication may take on new forms and complexities, but its core principles will remain a foundation of digital computation.
FAQ Section

What's the key difference between binary and decimal multiplication?
+Binary multiplication involves only the digits 0 and 1, whereas decimal multiplication uses the digits 0 to 9. The process is similar, but binary multiplication requires bitwise operations, making it simpler in terms of digit combinations.
How do I handle larger binary numbers in multiplication?
+For larger binary numbers, ensure you have a sufficiently large multiplication grid to accommodate all the digits. The process remains the same, but the scale increases.
Can binary multiplication be done mentally, or is it always done with a grid?
+Binary multiplication can be done mentally for smaller numbers, but for larger numbers, a grid or digital calculator is often necessary to ensure accuracy.
Are there any shortcuts or tricks to simplify binary multiplication?
+While there are no universal shortcuts, understanding the patterns and practicing regularly can lead to faster, more efficient multiplication.
By mastering the art of binary multiplication, you gain a deeper understanding of the fundamental operations that power our digital world. It’s a crucial skill for anyone interested in the inner workings of computers and digital systems.



