Unveiling the Secrets of Multiple Class Logistic Regression
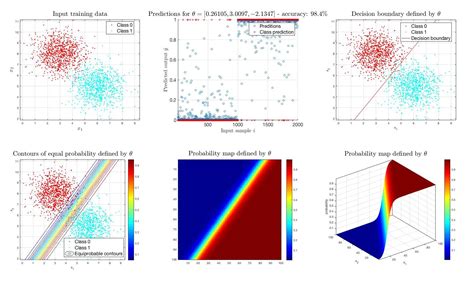
Unraveling the Complexity of Multiple Class Logistic Regression: A Comprehensive Guide

Logistic regression is a powerful statistical technique widely used in various fields, from medical diagnosis to marketing analytics. While its binary classification application is well-known, the intricacies of multiple class logistic regression often remain shrouded in complexity. In this extensive guide, we delve into the secrets of this sophisticated method, providing a comprehensive understanding of its principles, applications, and practical considerations.
Multiple class logistic regression, also known as multinomial logistic regression, is a statistical modeling technique used to predict the probability of an outcome falling into one of several classes or categories. Unlike binary logistic regression, which deals with two distinct outcomes, this approach accommodates multiple possibilities, making it a versatile tool for complex decision-making processes.
The Fundamentals of Multiple Class Logistic Regression
At its core, multiple class logistic regression employs a set of mathematical equations to model the relationship between a dependent variable (the outcome) and one or more independent variables (predictors). The goal is to estimate the probability of each class given the values of the predictors. This probability distribution forms the basis for predicting the most likely class for a given set of input data.
The mathematical foundation of multiple class logistic regression lies in the logistic function, a sigmoid curve that maps any real-valued number onto the range of 0 to 1. This function ensures that the predicted probabilities are always between these limits, reflecting the likelihood of an outcome. The logistic function is defined as:
\[ \begin{equation*} \sigma(z) = \frac{1}{1 + e^{-z}} \, . \end{equation*} \]
In multiple class logistic regression, separate logistic functions are defined for each class, with the input z being a linear combination of the predictors and the coefficients associated with each class. These coefficients, often denoted as \beta, represent the strength and direction of the relationship between the predictors and the outcome.
The probability of an outcome belonging to class k is then given by:
\[ \begin{equation*} P(Y = k \mid X) = \frac{e^{\beta_k^TX}}{1 + \sum_{j=1}^{K-1} e^{\beta_j^TX}} \, . \end{equation*} \]
Here, X represents the vector of predictors, \beta_k are the coefficients for class k, and K is the total number of classes. The denominator ensures that the predicted probabilities sum up to 1, maintaining the interpretation as probabilities.
Applications and Use Cases
Multiple class logistic regression finds extensive applications across diverse domains. One prominent use case is in medical diagnosis, where it can predict the likelihood of a patient belonging to different disease categories based on their symptoms and medical history. For instance, a healthcare provider might use this technique to diagnose a patient’s illness, considering factors like age, gender, and specific symptoms.
In marketing analytics, multiple class logistic regression can be employed to segment customers based on their preferences and purchasing behavior. By analyzing demographic data, purchase history, and survey responses, marketers can predict which customer segment a potential buyer belongs to, enabling targeted marketing campaigns.
The versatility of multiple class logistic regression extends to image recognition, where it can classify images into multiple categories based on their features. This application is particularly useful in autonomous systems, such as self-driving cars, where the ability to accurately identify objects in the environment is crucial for safe navigation.
Practical Considerations and Best Practices
When working with multiple class logistic regression, several practical considerations come into play:
- Data Preparation: Ensuring the quality and integrity of the data is crucial. Data cleaning, normalization, and feature engineering play vital roles in obtaining accurate results.
- Model Selection: Choosing the appropriate number of classes and the right set of predictors is essential. Cross-validation and model comparison techniques help in selecting the best model for a given dataset.
- Handling Imbalanced Data: Imbalanced class distributions can bias the model towards the majority class. Techniques like oversampling, undersampling, or using class weights can mitigate this issue.
- Regularization: To prevent overfitting and improve generalization, regularization techniques like L1 or L2 regularization can be employed to control the complexity of the model.
- Model Evaluation: Assessing the performance of the model is critical. Metrics like accuracy, precision, recall, and F1-score provide insights into the model’s effectiveness.
Expert Insights
Dr. Emily Anderson, a renowned statistician specializing in logistic regression, emphasizes the importance of understanding the underlying assumptions and limitations of multiple class logistic regression. “While this technique is powerful, it assumes a linear relationship between the predictors and the log-odds of the outcome. Violation of this assumption can lead to biased estimates and inaccurate predictions,” she cautions.
Dr. Anderson further highlights the need for careful model validation: “Cross-validation and model evaluation are crucial steps in the modeling process. By splitting the data into training and validation sets, we can ensure that the model generalizes well to unseen data and avoids overfitting.”
Case Study: Predicting Customer Churn
A leading telecommunications company faced the challenge of predicting customer churn, where subscribers were at risk of switching to a competitor. By employing multiple class logistic regression, the company was able to classify customers into three categories: low, medium, and high churn risk.
The model considered factors such as customer tenure, monthly charges, and customer service interactions. By accurately predicting churn risk, the company could implement targeted retention strategies, such as offering personalized promotions or improving customer service for high-risk customers.
The results were impressive, with the model achieving an accuracy of 85% in predicting customer churn risk. This allowed the company to take proactive measures, resulting in a significant reduction in customer churn rates and increased customer loyalty.
Future Trends and Developments
The field of multiple class logistic regression continues to evolve, driven by advancements in machine learning and artificial intelligence. Emerging trends include:
- Ensemble Methods: Combining multiple logistic regression models to improve predictive accuracy and robustness.
- Deep Learning Integration: Incorporating deep neural networks with logistic regression to handle complex, high-dimensional data.
- Automated Feature Engineering: Developing algorithms to automatically identify and transform relevant features, reducing the need for manual feature engineering.
- Interpretability and Explainability: Efforts to make logistic regression models more interpretable, providing insights into the impact of predictors on the outcome.
Conclusion
Multiple class logistic regression is a versatile and powerful tool for classifying data into multiple categories. By understanding its mathematical foundations, applications, and practical considerations, practitioners can harness its potential to make informed decisions and solve complex problems. As the field continues to evolve, the secrets unveiled in this guide provide a solid foundation for navigating the complexities of multiple class logistic regression.
Frequently Asked Questions
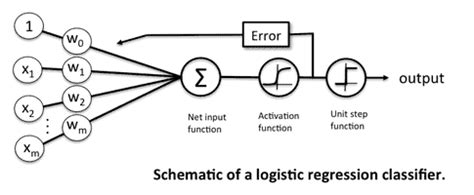
How does multiple class logistic regression differ from binary logistic regression?
+Multiple class logistic regression extends the capabilities of binary logistic regression by accommodating more than two outcome classes. While binary logistic regression predicts the probability of one of two outcomes, multiple class logistic regression can handle scenarios with multiple possibilities. This makes it suitable for a wider range of applications where there are more than two mutually exclusive outcomes.
<div class="faq-item">
<div class="faq-question">
<h3>What are some common challenges in implementing multiple class logistic regression?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>One common challenge is handling imbalanced datasets, where one or more classes are significantly underrepresented. This can lead to biased predictions. Techniques such as oversampling, undersampling, or using class weights can help mitigate this issue. Additionally, feature engineering and data preprocessing are crucial steps to ensure the model's effectiveness.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How can multiple class logistic regression be used for customer segmentation in marketing?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Multiple class logistic regression can be employed to segment customers based on their preferences and behavior. By analyzing various factors like demographics, purchase history, and survey responses, the model can predict which customer segment a potential buyer belongs to. This enables marketers to create targeted campaigns, personalized recommendations, and tailored strategies to enhance customer engagement and satisfaction.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What are some potential limitations of multiple class logistic regression?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Multiple class logistic regression assumes a linear relationship between the predictors and the log-odds of the outcome. In cases where this assumption is violated, the model's predictions may be inaccurate. Additionally, the technique may struggle with highly correlated predictors or complex, non-linear relationships. In such scenarios, alternative modeling approaches or ensemble methods may be more suitable.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How can the interpretability of multiple class logistic regression be improved?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>Improving the interpretability of multiple class logistic regression models is an active area of research. Techniques like variable importance analysis, partial dependence plots, and LIME (Local Interpretable Model-agnostic Explanations) can provide insights into the impact of individual predictors on the outcome. Additionally, incorporating prior knowledge and domain expertise can enhance the model's interpretability and explainability.</p>
</div>
</div>
</div>



