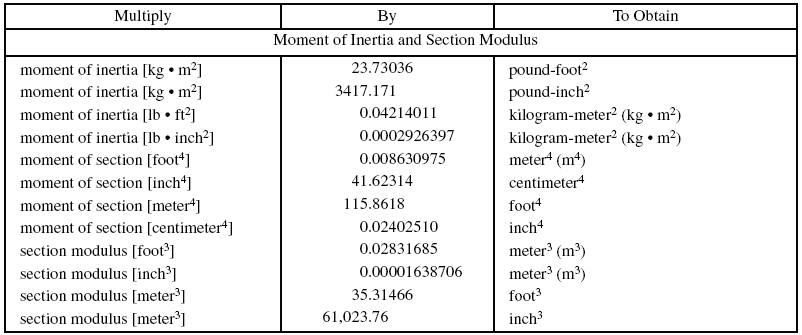
Understanding the Units of Moment of Inertia
Moment of inertia is a fundamental concept in physics and engineering, playing a crucial role in understanding rotational motion and the stability of objects. The units associated with moment of inertia are essential for accurate calculations and predictions. In this comprehensive guide, we’ll delve into the intricacies of these units, their definitions, and their significance in various contexts.
The Basics of Moment of Inertia
Moment of inertia, often denoted as I, is a measure of an object’s resistance to rotational acceleration. It is akin to how mass resists linear acceleration; the higher the moment of inertia, the more resistant an object is to changes in its rotational motion. This property is particularly important in fields such as mechanical engineering, aerospace, and physics, where the stability and behavior of rotating objects are critical considerations.
The Rotational Equation of Motion
The equation that governs rotational motion is akin to Newton’s second law for linear motion:
\[ \begin{equation*} \sum \tau = I \alpha \, . \end{equation*} \]
Here, \sum \tau represents the sum of torques acting on an object, I is the moment of inertia, and \alpha is the angular acceleration. This equation highlights the relationship between the applied torques, the object’s resistance to rotation (moment of inertia), and the resulting angular acceleration.
Units of Moment of Inertia

The units of moment of inertia are derived from the fundamental units of mass, length, and time. In the International System of Units (SI), the standard unit for moment of inertia is the kilogram-meter squared (\text{kg}\cdot\text{m}^2). However, in different contexts and systems of units, alternative units may be used. Let’s explore some of these units and their applications.
SI Units
In the SI system, the moment of inertia is measured in \text{kg}\cdot\text{m}^2. This unit is consistent with the SI base units, making it a natural choice for many scientific and engineering calculations. For example, consider a solid cylinder with a mass of 2 \text{ kg} and a radius of 0.1 \text{ m}. Its moment of inertia about its central axis would be:
\[ \begin{equation*} I = \frac{1}{2} m r^2 = \frac{1}{2} \times 2 \text{ kg} \times (0.1 \text{ m})^2 = 0.01 \text{ kg}\cdot\text{m}^2 \, . \end{equation*} \]
English Engineering Units
In the English Engineering system, the unit for moment of inertia is the slug-foot squared (\text{slug}\cdot\text{ft}^2). This unit is derived from the English units for mass (slug) and length (foot). While less commonly used today, it is still encountered in older engineering literature and some specialized fields.
Consistent Units for Rotational Motion
It is crucial to maintain consistent units when working with rotational motion equations. For example, if torques are measured in \text{N}\cdot\text{m}, then the moment of inertia should be in \text{kg}\cdot\text{m}^2 to ensure dimensional consistency. Converting between different units of moment of inertia is a common task, and understanding these conversions is essential for accurate calculations.
Dimensional Analysis for Moment of Inertia
From a dimensional analysis perspective, the moment of inertia can be expressed as:
\[ \begin{equation*} [I] = [M] \cdot [L]^2 \, , \end{equation*} \]
where [M] represents mass and [L] represents length. This expression underscores the fundamental relationship between mass and length in defining the moment of inertia.
Practical Applications of Moment of Inertia Units
The units of moment of inertia have wide-ranging practical applications in various fields:
- Mechanical Engineering: In designing rotating machinery like turbines, engines, and gears, precise calculations of moment of inertia are essential for optimizing performance and stability.
- Aerospace Engineering: Aircraft and spacecraft designs rely on accurate moment of inertia calculations for balancing and control systems.
- Physics: Understanding moment of inertia is crucial for studying rotational dynamics in physics, from simple pendulums to complex celestial bodies.
- Civil Engineering: In structural analysis, moment of inertia is used to assess the stability and strength of beams, columns, and other structural elements.
Advanced Concepts and Extensions
As we delve deeper into the study of moment of inertia, several advanced concepts and extensions come into play:
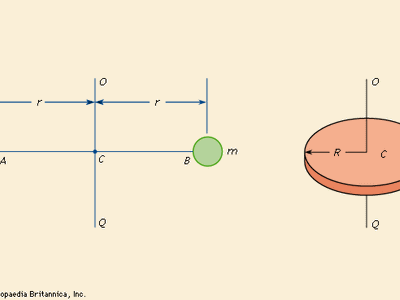
- Parallel Axis Theorem: This theorem allows us to calculate the moment of inertia about any axis parallel to the object’s original axis. It is particularly useful when analyzing composite objects.
- Principal Axes of Inertia: These are the axes about which the moment of inertia is the least or the most. Identifying these axes is crucial for simplifying complex rotational problems.
- Tensor Representation: In more advanced treatments of rotational motion, the moment of inertia is often represented as a tensor, providing a more general and powerful framework for analysis.
Key Takeaways

- Moment of inertia is a fundamental property of objects, measuring their resistance to rotational acceleration.
- The SI unit for moment of inertia is \text{kg}\cdot\text{m}^2, while other systems like English Engineering use \text{slug}\cdot\text{ft}^2.
- Consistent unit usage is vital for accurate calculations in rotational dynamics.
- The moment of inertia has practical applications in various engineering and scientific fields, impacting design, stability, and control systems.
- Advanced concepts like the parallel axis theorem and tensor representation extend our understanding of moment of inertia for complex scenarios.
FAQ
How does moment of inertia relate to an object’s mass and shape?
+The moment of inertia depends on both the mass distribution and the shape of an object. Objects with mass concentrated farther from the axis of rotation have higher moments of inertia, making them more resistant to rotational changes.
Why is consistent unit usage important in rotational motion calculations?
+Consistent unit usage ensures that all quantities in rotational motion equations, such as torques and moments of inertia, have compatible dimensions. This prevents errors and ensures accurate predictions of rotational behavior.
What are some real-world examples of moment of inertia in action?
+Moment of inertia is evident in everyday scenarios like a spinning top maintaining its balance, a figure skater increasing or decreasing their spin rate by pulling in or extending their arms, and the stability of a rotating wheel in a vehicle.
How do engineers use moment of inertia calculations in practical design?
+Engineers use moment of inertia calculations to optimize the design of rotating machinery, ensuring efficient performance and stability. For example, in designing a flywheel, engineers calculate the moment of inertia to achieve the desired rotational energy storage capacity.
Can moment of inertia change with the axis of rotation?
+Yes, the moment of inertia is dependent on the axis of rotation. Changing the axis can significantly alter the moment of inertia, as seen in the parallel axis theorem. This theorem allows us to calculate the moment of inertia about any parallel axis, which is crucial for analyzing composite objects.



