Understanding the Moment of Inertia: 5 Key Insights

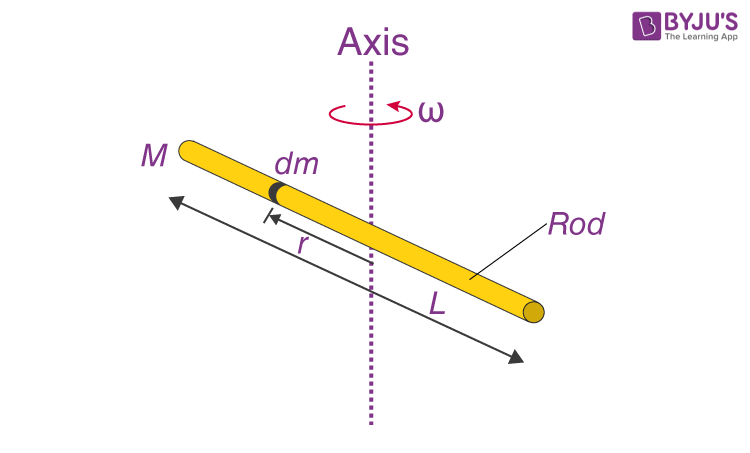
1. The Concept of Inertia

Inertia, a fundamental principle in physics, describes an object’s resistance to changes in its state of motion. Whether it’s an object at rest or in motion, inertia is what keeps it going or remaining at rest. This concept forms the basis for understanding the moment of inertia, a crucial parameter in rotational motion.

2. Mathematical Representation

The moment of inertia is mathematically expressed as:

\[ \begin{equation*} I = \sum_{i=1}^{n} m_i \cdot r_i^2 \, . \end{equation*} \]

Here, I is the moment of inertia, m_i represents the mass of the i-th particle, and r_i is the distance of that particle from the axis of rotation. This equation highlights the relationship between an object’s mass distribution and its resistance to changes in rotational motion.

3. Factors Affecting Moment of Inertia

The moment of inertia is influenced by several factors:

• Mass Distribution: The way mass is distributed around the axis of rotation plays a significant role. Objects with mass concentrated closer to the axis have lower moments of inertia compared to those with mass farther away.

• Shape: The shape of an object also affects its moment of inertia. For instance, a solid disk and a hollow cylinder with the same mass and radius have different moments of inertia due to their distinct mass distributions.

• Axis of Rotation: The choice of the axis of rotation can significantly impact the moment of inertia. Changing the axis can lead to different values, emphasizing the importance of selecting the appropriate axis for a given scenario.

4. Practical Applications

Understanding the moment of inertia has wide-ranging applications:

• Engineering and Design: Engineers use moment of inertia calculations to design structures, vehicles, and machinery. It’s crucial for ensuring stability, optimizing performance, and preventing catastrophic failures.

• Physics and Astronomy: In celestial mechanics, the moment of inertia is vital for understanding the dynamics of rotating bodies like planets, stars, and galaxies. It helps predict their behavior and interactions.

• Sports and Athletics: The moment of inertia is relevant in sports equipment design. For example, in golf club design, the moment of inertia affects the club’s forgiveness and ability to correct off-center hits.

5. Moment of Inertia and Angular Momentum

The moment of inertia is intimately linked to angular momentum, another fundamental concept in rotational motion. Angular momentum, denoted as L, is given by:

\[ \begin{equation*} L = I \cdot \omega \, , \end{equation*} \]

where \omega is the angular velocity. This relationship highlights that an object with a higher moment of inertia requires more angular momentum to achieve the same angular velocity as an object with a lower moment of inertia.

Key Takeaway

The moment of inertia is a vital parameter in rotational dynamics, offering insights into an object’s resistance to changes in its rotational motion. Its mathematical representation, factors influencing its value, and practical applications make it a fundamental concept with wide-ranging implications in physics, engineering, and beyond.

Frequently Asked Questions (FAQs)

    <div class="faq-item">
        <div class="faq-question">
            <h3>Can the moment of inertia be negative?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>No, the moment of inertia is always a positive quantity. It represents the object's resistance to changes in rotational motion, and negative values would imply a tendency to spontaneously start rotating, which is physically impossible.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>How does the moment of inertia affect the stability of rotating objects?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>A higher moment of inertia contributes to greater stability in rotating objects. This is because it requires more external force or torque to change the object's rotational motion. In practical terms, objects with higher moments of inertia are less likely to topple or change their orientation unexpectedly.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>What is the significance of the moment of inertia in sports equipment design?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>In sports equipment design, the moment of inertia is crucial for optimizing performance and control. For instance, in golf clubs, a higher moment of inertia provides a larger "sweet spot," making the club more forgiving and allowing for more consistent shots, even when the ball is not struck at the ideal point.</p>
        </div>
    </div>
</div>