Guía práctica: medidas con datos no agrupados

En el campo de la estadística, la medición de datos no agrupados es una herramienta fundamental para comprender y analizar información en su forma más básica. Esta guía práctica explorará en profundidad el proceso de trabajar con datos no agrupados, desde su definición hasta su aplicación práctica en diversas situaciones.
¿Qué son los datos no agrupados y por qué son importantes?

Los datos no agrupados, también conocidos como datos crudos o datos sin procesar, son valores individuales o observaciones que se recopilan en su forma más simple. Cada dato es único y no está relacionado directamente con otros en la muestra. Por ejemplo, las puntuaciones individuales en un examen, las edades de un grupo de personas o las ventas diarias de una tienda son todos ejemplos de datos no agrupados.
La importancia de los datos no agrupados radica en su capacidad para proporcionar una visión detallada y precisa de una población o fenómeno en estudio. Al trabajar con estos datos, podemos identificar tendencias, calcular medidas estadísticas y realizar análisis rigurosos. Además, los datos no agrupados son esenciales para la construcción de distribuciones de frecuencia y la posterior creación de gráficos y tablas que resumen la información de manera visual.
Medidas descriptivas de los datos no agrupados

Para comprender mejor los datos no agrupados, se utilizan medidas estadísticas que describen sus características. Estas medidas incluyen:
Media aritmética
La media aritmética es la suma de todos los valores dividida por el número total de valores. Es una medida que describe el valor central de los datos. Por ejemplo, si tenemos las edades de un grupo de 10 personas: 25, 30, 22, 28, 35, 23, 27, 32, 29 y 24, la media aritmética sería 27,5 años.
Mediana
La mediana es el valor central de un conjunto de datos ordenados. Cuando se ordenan los datos de menor a mayor, la mediana es el valor que se encuentra en la posición central. Si hay un número par de valores, la mediana se calcula como el promedio de los dos valores centrales. Por ejemplo, si ordenamos las edades anteriores, la mediana sería 27 años.
Moda
La moda es el valor que aparece con mayor frecuencia en un conjunto de datos. En algunos casos, puede haber más de una moda si varios valores aparecen con la misma frecuencia máxima. Por ejemplo, en una muestra de calificaciones de exámenes con los siguientes valores: 75, 80, 80, 70, 90, 85, 75, la moda sería 75 y 80.
Rango
El rango es la diferencia entre el valor máximo y el mínimo en un conjunto de datos. Es una medida que indica la dispersión de los datos. Por ejemplo, en la muestra de edades mencionada anteriormente, el rango sería 35 - 22 = 13 años.
Varianza y desviación estándar
La varianza y la desviación estándar son medidas que describen la dispersión o variabilidad de los datos. La varianza se calcula como la suma de los cuadrados de las diferencias entre cada valor y la media, dividida por el número total de valores menos uno. La desviación estándar es la raíz cuadrada de la varianza. Estas medidas proporcionan información sobre cuán alejados están los valores de la media.
Ejemplos prácticos de medidas con datos no agrupados
Para ilustrar el uso de estas medidas, consideremos el siguiente ejemplo: se desea analizar las alturas de un grupo de estudiantes en una clase. Los datos de altura en centímetros son:
| Altura (cm) | Frecuencia |
|---|---|
| 150 | 2 |
| 155 | 4 |
| 160 | 6 |
| 165 | 8 |
| 170 | 3 |
| 175 | 1 |
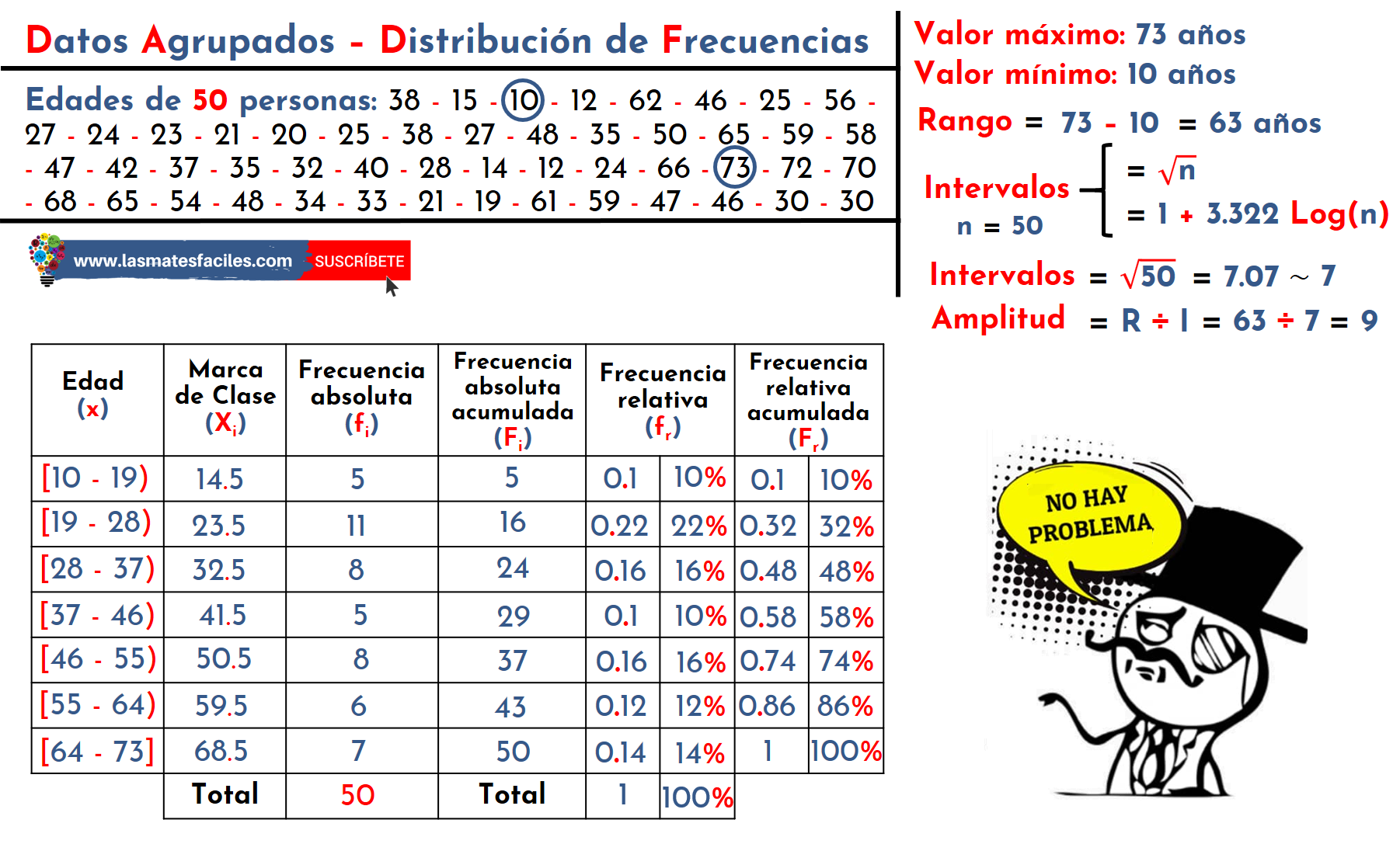
Cálculo de medidas
Media aritmética: (150 x 2) + (155 x 4) + (160 x 6) + (165 x 8) + (170 x 3) + (175 x 1) = 1314 / 24 = 54,75 cm.
Mediana: En este caso, la mediana se encuentra en el tercer cuartil, ya que el número de datos es impar. Ordenando los datos, obtenemos: 150, 150, 155, 155, 155, 160, 160, 160, 165, 165, 165, 170, 175. La mediana es 160 cm.
Moda: La moda en este ejemplo es 160 cm, ya que es el valor que aparece con mayor frecuencia.
Rango: El rango es 175 - 150 = 25 cm.
Varianza: (150 - 54,75)² + (150 - 54,75)² + … + (175 - 54,75)² = 1444,84. La varianza es 1444,84 / (24 - 1) = 62,66.
Desviación estándar: La desviación estándar es la raíz cuadrada de la varianza, es decir, √62,66 = 7,92 cm.
Aplicaciones prácticas
Las medidas descriptivas con datos no agrupados tienen una amplia gama de aplicaciones en diversos campos. En la investigación científica, se utilizan para analizar y presentar resultados de experimentos o estudios. En negocios y finanzas, son esenciales para comprender el desempeño de productos o servicios. En medicina, ayudan a evaluar la efectividad de tratamientos. Además, son fundamentales en la toma de decisiones informadas en áreas como la educación, la economía y la planificación urbana.
Conclusión
Los datos no agrupados son la base para comprender y analizar cualquier tipo de información cuantitativa. Al familiarizarnos con medidas como la media, la mediana, la moda, el rango y la desviación estándar, podemos describir y comprender mejor los datos en su forma más básica. Estas medidas nos permiten identificar patrones, comparar conjuntos de datos y realizar análisis estadísticos rigurosos. La capacidad de trabajar con datos no agrupados es una habilidad valiosa en cualquier campo que requiera el manejo y análisis de información.
¿Cuál es la diferencia entre datos agrupados y no agrupados?
+Los datos agrupados son aquellos que se organizan en categorías o intervalos, mientras que los datos no agrupados son valores individuales sin organización previa.
¿Se pueden calcular medidas estadísticas con datos no agrupados?
+Sí, las medidas estadísticas como la media, la mediana y la moda se pueden calcular directamente con datos no agrupados.
¿Qué sucede si tengo un conjunto de datos muy grande?
+Con conjuntos de datos grandes, puede ser más eficiente utilizar software estadístico para calcular las medidas y realizar análisis avanzados.



