Understanding the Difference: Mean vs Median

What is the Mean?

The mean, often referred to as the average, is a fundamental concept in mathematics and statistics. It represents the central value of a set of numbers, calculated by adding up all the values and then dividing by the total count. The mean provides a single numerical value that summarizes the entire dataset.

For instance, let’s consider a class of 10 students with the following test scores: 85, 90, 78, 92, 88, 75, 95, 80, 82, and 98. The mean score for this class can be calculated as:

(85 + 90 + 78 + 92 + 88 + 75 + 95 + 80 + 82 + 98) \div 10 = 84.4

So, the mean test score for this class is 84.4.

Pros and Cons of Using the Mean:

• Advantages:

  • The mean is easy to calculate and understand, making it a simple and intuitive measure of central tendency.
  • It is suitable for datasets with a normal distribution, where most values cluster around the mean.
  • The mean provides a single value that represents the average, making it convenient for comparison.

• Disadvantages:

  • The mean can be influenced by extreme values or outliers, potentially skewing the result.
  • It may not accurately reflect the typical value in datasets with a skewed distribution or significant variability.
  • In certain cases, the mean may not provide a meaningful representation, especially when dealing with ordinal or categorical data.

Exploring the Median

The median is another important measure of central tendency, offering a different perspective on the central value of a dataset. It is calculated by finding the middle value when the data is arranged in ascending or descending order. If there are an even number of values, the median is the average of the two middle numbers.

Using the same class of 10 students, let’s find the median test score:

Arranging the scores in ascending order: 75, 78, 80, 82, 85, 88, 90, 92, 95, 98.

Since there are an even number of values, the median is the average of the two middle numbers: (85 + 88) \div 2 = 86.5.

So, the median test score for this class is 86.5.

Understanding the Median’s Advantages:

• The median is less influenced by extreme values or outliers, making it a more robust measure in datasets with significant variability.
• It provides a good representation of the typical value, especially in skewed distributions.
• The median is particularly useful when dealing with ordinal or categorical data, as it doesn’t require numerical calculations.

When to Choose the Median:

• If your dataset contains outliers or extreme values, the median can provide a more accurate representation of the central tendency.
• In situations where you want to avoid the impact of extreme values, such as income or salary distributions, the median is a preferred choice.
• When dealing with ordinal or categorical data, the median is the appropriate measure, as it doesn’t rely on numerical calculations.

Mean vs Median: A Comparative Analysis

The choice between using the mean or median depends on the specific characteristics of your dataset and the context in which you are analyzing the data.

Mean’s Strengths:

• The mean is a simple and intuitive measure, easy to calculate and understand.
• It provides a single numerical value that represents the average, making it convenient for comparison.
• The mean is suitable for datasets with a normal distribution, where most values cluster around the mean.

Median’s Strengths:

• The median is less affected by extreme values or outliers, making it a more robust measure.
• It provides a good representation of the typical value, especially in skewed distributions.
• The median is ideal for ordinal or categorical data, as it doesn’t require numerical calculations.

When to Use Both:

In some cases, using both the mean and median can provide a more comprehensive understanding of your data. For example:

• If you have a dataset with a normal distribution, the mean will likely provide an accurate representation. However, calculating the median can still be beneficial to ensure that outliers aren’t skewing the results.
• In datasets with significant variability or skewed distributions, the median is the preferred measure. Still, calculating the mean can provide additional context, especially when comparing with other datasets.

A Real-World Example:

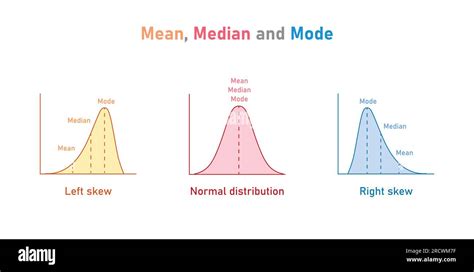
Let’s consider a study on household income. The mean income provides an overall average, but it can be skewed by a few extremely high-income households. In this case, the median income offers a more accurate representation of the typical household’s income.

In summary, both the mean and median have their strengths and are suitable for different scenarios. Understanding the characteristics of your dataset and the context of your analysis will guide you in choosing the most appropriate measure of central tendency.

FAQ Section: