Unveiling the Power of Mean Squared Error

Mean Squared Error (MSE) is a statistical measure that plays a crucial role in various fields, particularly in machine learning and data analysis. It provides valuable insights into the accuracy and performance of predictive models, allowing us to quantify and improve their effectiveness. In this article, we delve into the world of MSE, exploring its definition, significance, and practical applications. By understanding the power of MSE, we can unlock new dimensions of data-driven decision-making and enhance the precision of our predictive models.
Understanding Mean Squared Error: A Definition

At its core, Mean Squared Error is a metric used to evaluate the quality of predictions made by a model. It quantifies the average of the squared differences between the predicted values and the actual, observed values. Mathematically, MSE is calculated as follows:
\[ \text{MSE} = \frac{1}{n} \sum_{i=1}^{n} (y_i - \hat{y_i})^2 \]
Here, y_i represents the actual value, \hat{y_i} is the predicted value, and n is the total number of data points. By squaring the differences, MSE assigns a greater weight to larger errors, making it a sensitive measure of prediction accuracy.
The Significance of Mean Squared Error
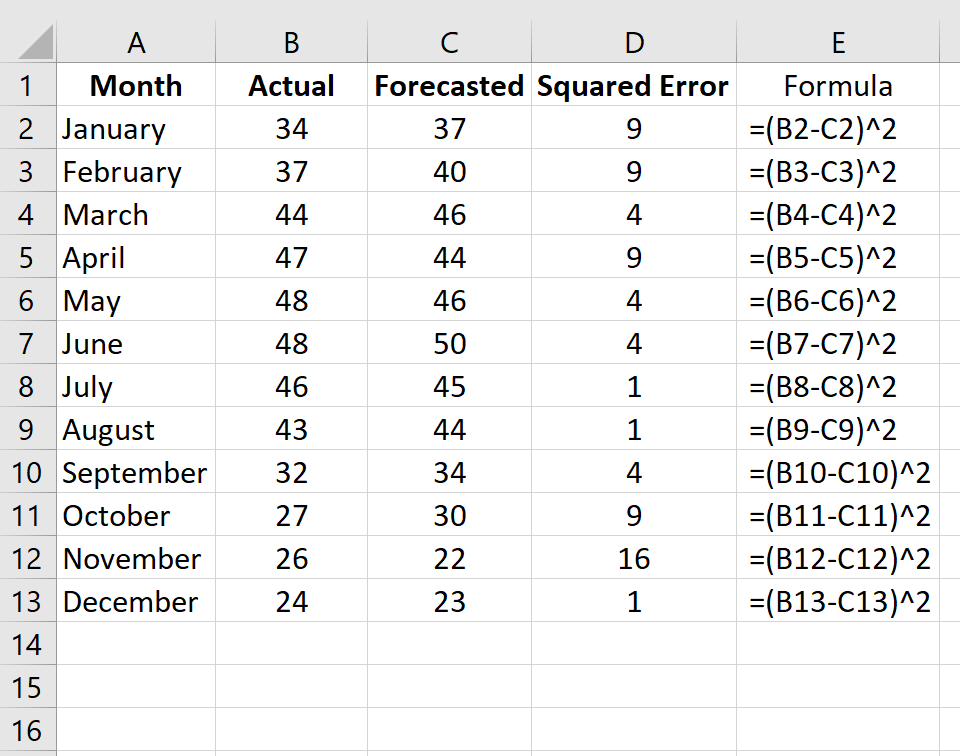
MSE holds immense importance in the realm of data analysis and machine learning for several reasons:
- Quantifying Model Performance: MSE provides a numerical representation of how well a model’s predictions align with the actual data. A lower MSE indicates better performance, as it signifies that the model’s predictions are closer to the observed values.
- Model Comparison: When evaluating multiple models, MSE allows for a fair and objective comparison. By calculating the MSE for each model, analysts can identify the most accurate and reliable predictive approach.
- Model Improvement: MSE serves as a powerful tool for model refinement. By identifying areas where the model’s predictions deviate significantly from the actual values, data scientists can focus their efforts on improving specific aspects of the model, such as feature engineering or hyperparameter tuning.
- Risk Assessment: In financial and economic contexts, MSE is invaluable for risk assessment. By measuring the squared errors, analysts can quantify the potential financial losses or gains associated with a model’s predictions, enabling better decision-making and risk management.
Practical Applications of Mean Squared Error
The versatility of MSE extends across various domains, making it a fundamental concept in many fields:
Machine Learning
In machine learning, MSE is a widely used metric for evaluating regression models. Whether it’s predicting stock prices, sales forecasts, or climate patterns, MSE helps assess the accuracy of these models and guides their optimization.
Image Processing
MSE finds applications in image processing tasks, such as image restoration and compression. By calculating the MSE between the original and processed images, researchers can quantify the quality of image enhancement algorithms and make informed decisions about image processing techniques.
Quality Control
In manufacturing and quality control, MSE is employed to assess the accuracy of measurement systems. By comparing the measured values with the reference values, MSE helps identify any biases or errors in the measurement process, ensuring product quality and reliability.
Financial Forecasting
Financial analysts utilize MSE to evaluate the performance of predictive models in forecasting stock prices, interest rates, and economic indicators. A lower MSE indicates a more accurate model, providing valuable insights for investment decisions.
Medical Diagnosis
In the medical field, MSE is applied to evaluate the accuracy of diagnostic models. By comparing predicted diagnoses with actual patient outcomes, MSE assists in refining diagnostic algorithms and improving patient care.
Case Study: Mean Squared Error in Climate Modeling
Let’s explore a real-world application of Mean Squared Error in climate modeling. Climate scientists often use predictive models to forecast future climate patterns and understand the impact of various factors on the Earth’s climate system.
Through iterative refinement and validation using MSE, the climate researchers were able to develop a robust climate model that provided valuable insights into future climate trends. The model’s predictions, combined with other climate analysis techniques, contributed to a better understanding of the Earth’s changing climate and informed policy decisions aimed at mitigating climate change impacts.
Future Trends and Developments

As data-driven technologies continue to advance, Mean Squared Error is likely to remain a cornerstone metric in various fields. However, researchers are also exploring alternative error metrics and evaluation techniques to address specific challenges and improve model performance.
Conclusion
Mean Squared Error is a versatile and impactful metric, empowering data scientists, researchers, and analysts across diverse domains. By understanding its definition, significance, and practical applications, we can harness the power of MSE to make more accurate predictions, refine models, and drive informed decision-making. As data continues to shape our world, MSE remains a fundamental tool in the arsenal of data-driven professionals, unlocking new possibilities and insights.
How does Mean Squared Error differ from other error metrics like Mean Absolute Error (MAE)?
+Mean Squared Error (MSE) and Mean Absolute Error (MAE) are both used to evaluate the performance of predictive models, but they differ in their approach. MSE assigns a greater weight to larger errors due to the squaring of differences, making it more sensitive to outliers. MAE, on the other hand, calculates the average of the absolute differences, providing a more balanced measure that is less influenced by extreme values. The choice between MSE and MAE depends on the specific requirements of the analysis and the characteristics of the data.
Can Mean Squared Error be used for classification tasks, or is it only applicable to regression problems?
+Mean Squared Error is primarily used for regression tasks, where the goal is to predict continuous numerical values. In classification problems, where the target variable is categorical, other evaluation metrics like accuracy, precision, recall, or F1-score are more commonly employed. However, in certain scenarios, such as multi-class classification with probabilistic outputs, MSE can still be used as an evaluation metric.
How does MSE handle imbalanced datasets, where certain classes or outcomes are underrepresented?
+MSE can be affected by imbalanced datasets, as it assigns equal weight to each data point. In such cases, the model’s performance may be biased towards the majority class. To mitigate this issue, techniques like class weighting or resampling can be applied to balance the dataset and ensure fair evaluation. Additionally, alternative error metrics like Mean Absolute Percentage Error (MAPE) or Median Absolute Error (MedAE) may provide more robust evaluations in imbalanced scenarios.
Is a lower Mean Squared Error always indicative of a better model?
+A lower MSE generally suggests a more accurate model, as it indicates that the predicted values are closer to the actual values. However, it’s important to interpret MSE in the context of the specific problem and dataset. In some cases, a lower MSE may not necessarily imply a better model if the dataset has inherent noise or if the model is overly simplified. It’s crucial to consider other evaluation metrics and domain-specific considerations to gain a comprehensive understanding of model performance.
Are there any alternative error metrics or evaluation techniques that can complement Mean Squared Error?
+Yes, there are several alternative error metrics and evaluation techniques that can provide additional insights. Some commonly used alternatives include Mean Absolute Error (MAE), Mean Absolute Percentage Error (MAPE), Median Absolute Error (MedAE), and R-squared (R2). Additionally, techniques like cross-validation, bootstrapping, or ensemble methods can be employed to assess model performance and generalizability. It’s beneficial to consider a combination of metrics and techniques to gain a holistic understanding of model accuracy and reliability.


