4 Easy Steps to Understand Maxwell-Boltzmann
Understanding the Maxwell-Boltzmann Distribution: A Guide to Statistical Mechanics

Grasping the Maxwell-Boltzmann distribution is an essential milestone in the realm of statistical mechanics. This fundamental concept provides insights into the behavior of gas particles at the microscopic level. Let’s embark on a journey to demystify this topic, breaking it down into manageable steps.
Step 1: Laying the Foundation
The Maxwell-Boltzmann distribution is a statistical model that describes the velocities of particles in an ideal gas. It forms a cornerstone of statistical mechanics, a branch of physics that deals with the behavior of large numbers of particles and their collective properties. To comprehend this distribution, we first need to familiarize ourselves with the key players: particles and their velocities.
In an ideal gas, particles are assumed to be point masses that collide elastically with each other and the walls of their container. These particles are in constant, random motion, and their velocities play a pivotal role in determining the gas’s macroscopic properties, such as pressure and temperature.
Step 2: Delving into the Distribution
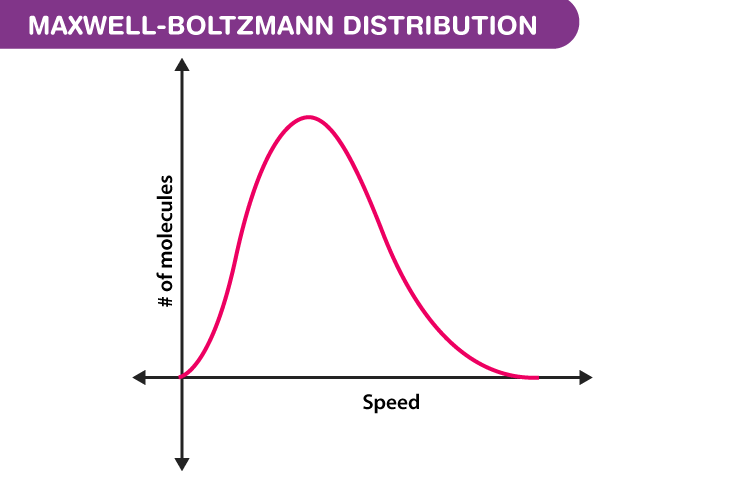
The Maxwell-Boltzmann distribution provides a probability distribution function that describes the likelihood of finding a particle with a certain velocity. This function is shaped like a bell curve, with the highest probability corresponding to the most probable velocity. The curve’s shape is influenced by factors like temperature and the mass of the gas particles.
Mathematically, the Maxwell-Boltzmann distribution is expressed as:
\[ \begin{equation*} f(v) = \left(\frac{m}{2\pi kT}\right)^{3/2} \cdot 4\pi v^2 \cdot e^{-\frac{mv^2}{2kT}} \end{equation*} \]
where: - f(v) is the probability density function, - m is the mass of a gas particle, - k is the Boltzmann constant, - T is the absolute temperature, and - v is the velocity of the particle.
This equation might look daunting, but its components are essential for understanding the distribution. The mass of the particle affects how its velocity is distributed, with heavier particles tending to move slower. The Boltzmann constant relates the temperature to the kinetic energy of the particles, influencing the overall spread of velocities.
Step 3: Interpreting the Distribution’s Implications
The Maxwell-Boltzmann distribution has far-reaching implications in the study of gases. For instance, it allows us to calculate the root mean square velocity of gas particles, which is a measure of their average kinetic energy. This velocity is directly proportional to the square root of the absolute temperature.
\[ \begin{equation*} v_{\text{rms}} = \sqrt{\frac{3kT}{m}} \end{equation*} \]
This equation provides a powerful tool for relating the microscopic properties of gas particles (their velocities) to the macroscopic properties we can observe and measure (temperature and pressure).
Step 4: Applying the Distribution in Practice
The Maxwell-Boltzmann distribution finds practical applications in various fields. For instance, it’s crucial in the study of chemical kinetics, where it helps predict reaction rates based on the velocities of reacting particles. In engineering, it’s used to design and optimize gas turbines and internal combustion engines.
Consider a scenario where engineers are designing a new aircraft engine. They need to understand how the gas particles behave inside the engine’s combustion chamber. By applying the Maxwell-Boltzmann distribution, they can predict the average velocity of these particles, which is crucial for determining the engine’s performance and efficiency.
In conclusion, the Maxwell-Boltzmann distribution is a powerful tool in the physicist’s toolkit. It allows us to peer into the microscopic world of gas particles and understand their collective behavior. By following these four steps, you’re well on your way to mastering this fundamental concept in statistical mechanics.
Frequently Asked Questions

How does the Maxwell-Boltzmann distribution relate to the kinetic theory of gases?
+The Maxwell-Boltzmann distribution is a direct consequence of the kinetic theory of gases. This theory postulates that gases consist of a large number of particles in constant, random motion, and their collective behavior leads to observable gas properties. The distribution provides a mathematical description of this theory, allowing us to predict the velocities of these particles and, consequently, the macroscopic properties of gases.
<div class="faq-item">
<div class="faq-question">
<h3>Can the Maxwell-Boltzmann distribution be applied to real gases, or is it limited to ideal gases?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>While the Maxwell-Boltzmann distribution is primarily derived for ideal gases, it can still provide valuable insights for real gases. However, it's important to note that real gases deviate from ideal behavior at high pressures and low temperatures. In such cases, more advanced distributions, like the Maxwell-Boltzmann-Dirac distribution or the Maxwell-Boltzmann-Fermi distribution, may be more appropriate.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>What happens to the Maxwell-Boltzmann distribution at extremely low temperatures?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>At extremely low temperatures, the Maxwell-Boltzmann distribution starts to break down. This is because, as temperature decreases, the thermal energy of the gas particles becomes comparable to their quantum mechanical energies. In such scenarios, the Boltzmann distribution must be modified to account for quantum effects, leading to the emergence of the Maxwell-Boltzmann-Dirac distribution.</p>
</div>
</div>
<div class="faq-item">
<div class="faq-question">
<h3>How does the Maxwell-Boltzmann distribution change with the mass of the gas particles?</h3>
<span class="faq-toggle">+</span>
</div>
<div class="faq-answer">
<p>The mass of the gas particles directly affects the shape of the Maxwell-Boltzmann distribution. Heavier particles tend to have lower velocities on average, resulting in a narrower distribution. Conversely, lighter particles exhibit higher velocities, leading to a broader distribution. This relationship is reflected in the mathematical expression of the distribution, where the mass term influences the curve's shape.</p>
</div>
</div>
</div>



