Unveiling the Secret: Maximum Value Theorem
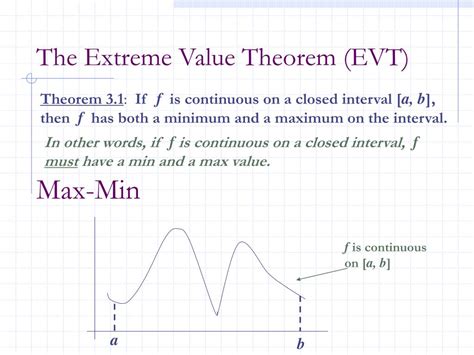
The concept of the Maximum Value Theorem, often referred to as the “Extreme Value Theorem,” is a fundamental principle in calculus that has wide-ranging applications across various fields. It provides a mathematical foundation for understanding and predicting the behavior of functions, making it an essential tool for anyone working with data analysis, optimization, or problem-solving. This theorem, despite its seemingly technical nature, has profound implications and real-world relevance.
At its core, the Maximum Value Theorem states that for a continuous function on a closed interval, there exists a maximum and a minimum value. This may seem intuitive, but its implications are far-reaching and offer a powerful tool for understanding and manipulating data.
Imagine a function as a rollercoaster ride, with its peaks and valleys representing the highest and lowest points. The Maximum Value Theorem tells us that, given a closed interval, there will always be a highest point (maximum) and a lowest point (minimum). This insight is incredibly valuable, especially when dealing with real-world data that often has its ups and downs.
Historical Evolution: From Concept to Theorem

The journey of the Maximum Value Theorem began with the foundational work of mathematicians in the 17th and 18th centuries. During this period, calculus was emerging as a powerful tool for understanding the world, and mathematicians like Newton and Leibniz were laying the groundwork for what we now know as the Extreme Value Theorem.
Pro: Early Intuition
Even in the early days of calculus, mathematicians understood the basic principle that functions had maximum and minimum values. This intuition, however crude, laid the foundation for future exploration.
Con: Lack of Rigor
While the early mathematicians had a grasp of the concept, their understanding lacked the mathematical rigor we expect today. The formal proof and precise definition of the theorem were yet to come.
It was in the 19th century that the theorem took its modern form. Mathematicians like Cauchy and Weierstrass refined the concept, providing a more precise definition and proof. Their work formalized the understanding of extreme values, ensuring its reliability and applicability across various fields.
Real-World Applications: Maximum Value Theorem in Action

The Maximum Value Theorem is not just a theoretical concept; it has a wide range of practical applications that impact our daily lives. Here are some real-world scenarios where this theorem plays a crucial role:
Economic Analysis: In economics, the theorem is used to identify the optimal production level, where the maximum profit can be achieved. It helps economists and businesses make informed decisions about production strategies.
Engineering: Engineers use the theorem to find the maximum or minimum values of various functions, such as stress or strain in materials. This information is vital for designing safe and efficient structures.
Quality Control: In manufacturing, the theorem is employed to set control limits for product quality. By identifying the maximum and minimum acceptable values, manufacturers can ensure consistent product quality.
Environmental Science: Ecologists and environmental scientists use the theorem to model population growth or the spread of pollutants. It helps in predicting the maximum population a habitat can support or the minimum amount of pollution that can cause ecological damage.
Comparative Analysis: Maximum Value Theorem vs. Other Optimization Methods
While the Maximum Value Theorem is a powerful tool, it’s not the only method for optimization. Here’s a comparative analysis of the theorem against other popular optimization techniques:
| Maximum Value Theorem | Other Optimization Methods |
|---|---|
|
|

While other methods have their strengths, the Maximum Value Theorem stands out for its simplicity and broad applicability. It provides a foundational understanding of optimization, making it an essential first step for anyone venturing into more advanced optimization techniques.
Future Trends: Maximum Value Theorem in Emerging Fields
As we move forward into the 21st century, the Maximum Value Theorem continues to find new applications in emerging fields. Here’s a glimpse into the future:
Artificial Intelligence: In AI, the theorem can be used to optimize machine learning algorithms, helping them learn more efficiently and make better predictions.
Big Data Analytics: With the explosion of data, the theorem can assist in identifying trends and patterns, ensuring data-driven decisions are based on extreme values.
Quantum Computing: As quantum computing advances, the theorem could play a role in optimizing quantum algorithms, harnessing the power of quantum systems.
Robotics: In robotics, the theorem can be used to optimize movement and energy efficiency, making robots more efficient and adaptable.
Practical Guide: Utilizing the Maximum Value Theorem

For those looking to apply the Maximum Value Theorem, here’s a step-by-step guide:
- Identify the function you want to analyze.
- Determine the closed interval on which the function is defined.
- Use the theorem to guarantee the existence of a maximum and minimum value.
- Apply optimization techniques to find the extreme values.
- Interpret the results in the context of your specific problem or application.
Remember, the Maximum Value Theorem is a powerful tool, but it’s just one part of the broader optimization toolkit. As with any mathematical concept, practice and real-world application are key to mastering its use.
FAQ
What is the significance of the Maximum Value Theorem in real-world applications?
+The theorem is significant because it provides a guarantee of extreme values for continuous functions on closed intervals. This guarantee is essential for making informed decisions and predictions in various fields, including economics, engineering, and environmental science.
Can the Maximum Value Theorem be applied to all functions?
+No, the theorem applies specifically to continuous functions on closed intervals. For functions that are not continuous or defined on open intervals, the theorem may not hold true, and alternative methods should be considered.
How does the Maximum Value Theorem compare to other optimization methods?
+The Maximum Value Theorem is a simple, intuitive method that guarantees the existence of extreme values. Other optimization methods may be more complex and technical, requiring additional assumptions or conditions. The choice of method depends on the specific problem and its requirements.
What are some potential limitations of the Maximum Value Theorem?
+The theorem assumes a continuous function on a closed interval. If these conditions are not met, the theorem may not apply. Additionally, while the theorem guarantees the existence of extreme values, it does not provide a method for finding them, which requires additional optimization techniques.
The Maximum Value Theorem is a fundamental tool in the calculus toolkit, offering a powerful understanding of extreme values. Its applications are diverse and far-reaching, impacting fields from economics to engineering and beyond. As we continue to explore the potential of this theorem, its relevance and utility only grow, ensuring its place as a cornerstone of mathematical understanding.



