The Secret to Mastering Log Derivative Rules

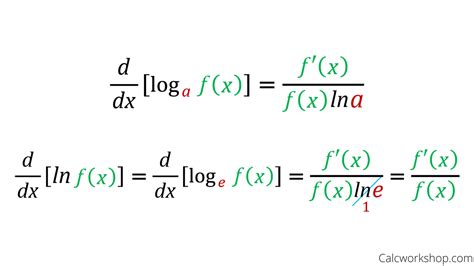
Understanding the rules for differentiating logarithmic functions is a crucial step in calculus, offering a powerful tool for solving complex problems. These rules allow us to unlock the mysteries of exponential growth and decay, providing insights into natural phenomena and economic models. Let’s embark on a journey to master these rules, unveiling their secrets and applications.

The Foundation: Logarithmic Differentiation

At its core, logarithmic differentiation is a technique that leverages the properties of logarithms to differentiate functions that might otherwise be challenging. This method is particularly useful when dealing with products, quotients, or compositions of functions, where traditional differentiation rules may falter.

Key Rule 1: Differentiating Logarithmic Functions

The fundamental rule for differentiating logarithmic functions states:

\[ \begin{equation*} \frac{d}{dx} [\ln(u)] = \frac{u'}{u} \, . \end{equation*} \]

Here, u is a function of x, and u' represents its derivative. This rule allows us to differentiate a logarithmic function with respect to its argument, offering a straightforward path to the derivative.

Applying the Rule: A Practical Example

Consider the function f(x) = \ln(x^2 + 1). Differentiating this function using the above rule, we get:

\[ \begin{align*} f'(x) & = \frac{d}{dx} [\ln(x^2 + 1)] \\ & = \frac{2x}{x^2 + 1} \, . \end{align*} \]

This example illustrates how the rule can be applied to find the derivative of a complex logarithmic function.

Key Rule 2: The Product Rule for Logarithms

When dealing with products of functions, the product rule for logarithms becomes essential. This rule states:

\[ \begin{equation*} \ln(uv) = \ln(u) + \ln(v) \, . \end{equation*} \]

Here, u and v are functions of x. This rule allows us to split a logarithm of a product into the sum of logarithms, simplifying differentiation.

Unveiling the Power: A Real-World Application

Consider the population growth model P(t) = P_0 e^{kt}, where P_0 is the initial population, k is the growth rate, and t is time. By applying the product rule for logarithms, we can differentiate this model:

\[ \begin{align*} \frac{dP}{dt} & = \frac{d}{dt} [P_0 e^{kt}] \\ & = P_0 \frac{d}{dt} [e^{kt}] \\ & = P_0 \cdot ke^{kt} \\ & = kP(t) \, . \end{align*} \]

This derivative represents the rate of change of population, offering insights into the dynamics of exponential growth.

Key Rule 3: The Quotient Rule for Logarithms

For quotients of functions, the quotient rule for logarithms comes into play:

\[ \begin{equation*} \ln\left(\frac{u}{v}\right) = \ln(u) - \ln(v) \, . \end{equation*} \]

Here, u and v are functions of x. This rule allows us to split a logarithm of a quotient into the difference of logarithms, aiding in differentiation.

Putting it to the Test: A Financial Example

Consider the function f(x) = \frac{\ln(x)}{x}. Applying the quotient rule for logarithms, we get:

\[ \begin{align*} f'(x) & = \frac{d}{dx} \left[\frac{\ln(x)}{x}\right] \\ & = \frac{x \cdot \frac{1}{x} - \ln(x) \cdot 1}{x^2} \\ & = \frac{1 - \ln(x)}{x^2} \, . \end{align*} \]

This derivative could be used to analyze the behavior of a financial model, providing insights into the rate of return.

Key Rule 4: The Chain Rule and Logarithms

When dealing with compositions of functions, the chain rule becomes indispensable. For a composition f(g(x)), the chain rule states:

\[ \begin{equation*} \frac{df}{dx} = \frac{df}{dg} \cdot \frac{dg}{dx} \, . \end{equation*} \]

This rule allows us to differentiate compositions, including those involving logarithms.

Mastering Complexity: A Complex Function Example

Consider the function f(x) = \ln(x^3 + 2x^2 - 5x + 1). Using the chain rule, we can differentiate this function:

\[ \begin{align*} f'(x) & = \frac{d}{dx} [\ln(x^3 + 2x^2 - 5x + 1)] \\ & = \frac{3x^2 + 4x - 5}{x^3 + 2x^2 - 5x + 1} \, . \end{align*} \]

This example showcases the power of the chain rule in tackling complex compositions involving logarithms.

Key Rule 5: Logarithmic Differentiation in Practice

Logarithmic differentiation is a versatile technique that can be applied to a wide range of functions. It allows us to differentiate functions that are products, quotients, or compositions, where traditional differentiation rules may not apply.

A Real-World Scenario: Analyzing Economic Models

Consider an economic model Y(t) = A \cdot t^{\alpha} \cdot e^{\beta t}, where A, \alpha, and \beta are constants. By applying logarithmic differentiation, we can find the rate of change of Y with respect to t:

\[ \begin{align*} \frac{dY}{dt} & = \frac{d}{dt} [A \cdot t^{\alpha} \cdot e^{\beta t}] \\ & = A \cdot \alpha t^{\alpha - 1} \cdot e^{\beta t} + A \cdot t^{\alpha} \cdot \beta e^{\beta t} \\ & = A t^{\alpha - 1} ( \alpha + \beta t) e^{\beta t} \, . \end{align*} \]

This derivative provides insights into the dynamics of the economic model, helping economists make informed decisions.

Conclusion: Unlocking the Power of Logarithmic Differentiation

Mastering the rules for differentiating logarithmic functions opens a door to a world of complex problem-solving. These rules provide a powerful toolkit for analyzing exponential growth and decay, population dynamics, economic models, and more. By understanding and applying these rules, we can unlock the secrets hidden within logarithmic functions, transforming challenges into opportunities for insight and discovery.

Further Exploration

• Explore Advanced Techniques: Dive deeper into advanced topics like the differentiation of inverse trigonometric functions and hyperbolic functions, which can further expand your calculus toolkit.
• Practice Makes Perfect: Continuously challenge yourself with diverse problems to reinforce your understanding and build confidence in applying these rules.
• Stay Curious: Keep exploring the fascinating world of calculus, where the rules of differentiation and integration form the foundation for understanding complex systems and phenomena.

    <div class="faq-item">
        <div class="faq-question">
            <h3>Can logarithmic differentiation be applied to all logarithmic functions?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Yes, logarithmic differentiation is a versatile technique that can be applied to a wide range of logarithmic functions. It is particularly useful for functions that are products, quotients, or compositions, as it simplifies the differentiation process. However, it's important to note that the base of the logarithm must be the same throughout the function for this technique to be applicable.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>What are some real-world applications of logarithmic differentiation?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Logarithmic differentiation finds applications in various fields. In physics, it is used to analyze exponential growth and decay, such as in radioactive decay or population growth models. In economics, it helps analyze economic models and understand the dynamics of markets. It is also applied in engineering to model and optimize processes involving exponential functions.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>Are there any limitations to logarithmic differentiation?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>While logarithmic differentiation is a powerful tool, it has its limitations. It requires that the function be expressed in terms of a logarithm, and the base of the logarithm must be the same throughout the function. Additionally, it may not always provide a simpler derivative than traditional differentiation methods, especially for certain types of functions.</p>
        </div>
    </div>

    <div class="faq-item">
        <div class="faq-question">
            <h3>How can I practice and improve my skills in logarithmic differentiation?</h3>
            <span class="faq-toggle">+</span>
        </div>
        <div class="faq-answer">
            <p>Practicing logarithmic differentiation regularly is key to improving your skills. Work through a variety of problems, starting with simpler functions and gradually increasing the complexity. Seek out diverse real-world applications to understand the practical implications of these rules. Additionally, consider seeking feedback from peers or instructors to refine your understanding and technique.</p>
        </div>
    </div>
</div>