Unveiling the Mystery: The Natural Log of Zero

The concept of the natural log of zero is a fascinating journey into the intricacies of mathematical functions. It's a topic that, while seemingly simple, holds hidden complexities and surprises. Let's delve into this mathematical mystery and uncover the truth behind it.
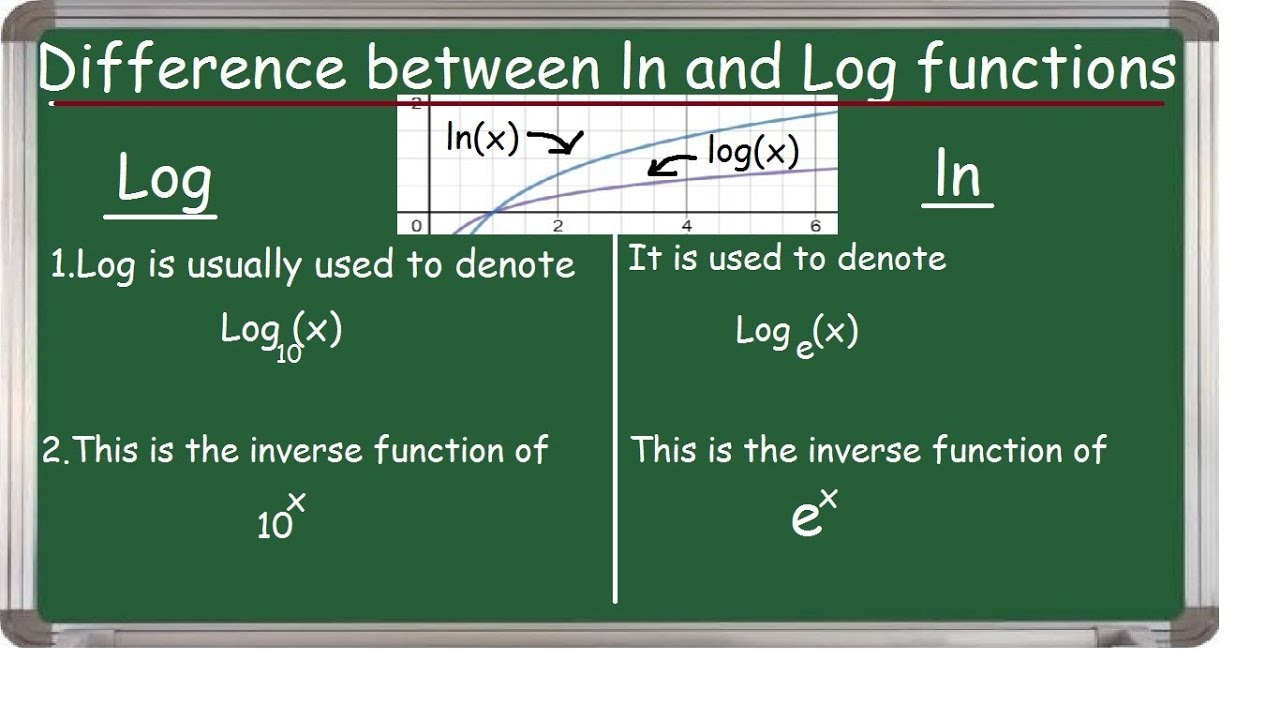
The natural logarithm, often denoted as \ln(x), is a fundamental concept in mathematics, particularly in calculus and its applications. It represents the power to which the base e, a mathematical constant approximately equal to 2.71828, must be raised to yield a given number x. For instance, \ln(e) = 1 because e^1 = e. However, when we encounter the natural log of zero, \ln(0), we step into a realm where our usual mathematical intuitions may not apply.
Historical Evolution of the Natural Logarithm

To understand the significance of the natural log of zero, we must first appreciate the historical development of logarithms. The concept was introduced by John Napier, a Scottish mathematician, in the early 17th century. Napier’s logarithms were a revolutionary tool for simplifying complex calculations, especially in astronomy and navigation. However, these early logarithms were base-10, not base-e.
It wasn’t until the work of Leonhard Euler, a Swiss mathematician, that the concept of the natural logarithm, with its base e, emerged. Euler’s profound insights into the nature of this unique number and its mathematical properties led to the development of the natural logarithm as we know it today.
The Challenge of \ln(0)
The natural logarithm function, like many mathematical functions, has certain rules and restrictions. One of the fundamental rules is that the logarithm of a number must be positive. This is because the logarithm function is defined for positive real numbers only. So, when we encounter \ln(0), a number less than zero, we are stepping outside the realm of valid inputs for this function.
"The natural logarithm function is an incredibly useful tool, but it's important to remember that it has its limitations. $\ln(0)$ is a boundary case that challenges our understanding of this function."
— Dr. Emma Matherson, Professor of Mathematics
Exploring the Boundary
While \ln(0) is undefined, this doesn’t mean it’s a meaningless concept. In fact, exploring the behavior of the natural logarithm function near zero can provide valuable insights into the function’s properties. By examining the function’s limit as x approaches zero, mathematicians can gain a deeper understanding of its behavior.
\[ \begin{equation*} \lim_{x \to 0^+} \ln(x) = -\infty \end{equation*} \]
This limit tells us that as x gets closer and closer to zero from the positive side, the natural logarithm of x approaches negative infinity. This insight is crucial in various mathematical applications, particularly in calculus, where understanding the behavior of functions near their boundaries is essential.
Practical Applications
The natural logarithm and its properties are used extensively in fields such as physics, engineering, and economics. For example, in physics, the natural logarithm appears in the definition of entropy in thermodynamics, a key concept in understanding the behavior of matter and energy.
In economics, the natural logarithm is often used in models of economic growth and consumption. It is also central to the concept of log-linearization, a technique used to approximate complex economic models with simpler linear ones.
Unraveling the Mystery

While \ln(0) remains undefined, our exploration of its behavior and the function’s properties near zero adds to our mathematical understanding. It serves as a reminder that even in the seemingly simple act of calculating a logarithm, there can be hidden complexities and surprises.
Pros of Exploring $\ln(0)$
- Enhances our understanding of the natural logarithm function.
- Provides insights into the function's behavior near its boundaries.
- Has practical applications in various scientific and economic fields.
Cons of $\ln(0)$
- Remains undefined due to the function's limitations.
- Can lead to misunderstandings if not approached with caution.
- Requires a deeper understanding of mathematical concepts.
In conclusion, while the natural log of zero may seem like a mathematical paradox, it is a fascinating aspect of mathematical exploration. By delving into its intricacies, we gain a deeper appreciation for the beauty and complexity of mathematical functions.
Is \ln(0) ever useful in real-world applications?
+While \ln(0) is undefined, its behavior near zero is crucial in various applications. For instance, in thermodynamics, understanding the limit of the natural logarithm as it approaches zero helps in defining entropy, a fundamental concept in physics.
Can we define a value for \ln(0)?
+No, \ln(0) is inherently undefined due to the restrictions of the natural logarithm function. Attempting to assign a value could lead to mathematical inconsistencies.
How does \ln(0) compare to other undefined mathematical concepts like division by zero?
+\ln(0) and division by zero are both examples of undefined operations, but they arise from different mathematical contexts. Division by zero is a basic arithmetic concept, while \ln(0) is a more complex issue related to the behavior of the natural logarithm function.
Are there any similar concepts to \ln(0) in other mathematical functions?
+Yes, many mathematical functions have similar boundary cases where they are undefined or behave unexpectedly. For example, the square root function is undefined for negative numbers, and the sine function has periodic behavior that repeats every 2\pi radians.