Signos: Ley de los signos para resolver ejercicios.

En el mundo de la matemática, la Ley de los Signos es una herramienta fundamental para resolver problemas y ejercicios algebraicos. Esta ley, también conocida como la Ley de los Signos de los Números, proporciona una guía clara para trabajar con operaciones que involucran signos positivos y negativos. A continuación, exploraremos en profundidad la Ley de los Signos, su importancia, y cómo aplicarla para resolver problemas matemáticos de manera eficiente.
La Ley de los Signos: Una Herramienta Poderosa
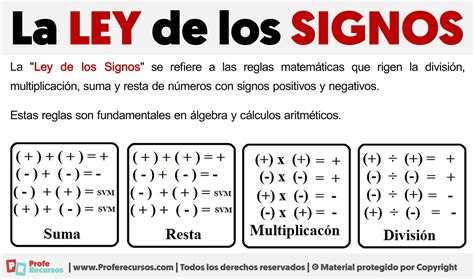
La Ley de los Signos establece una serie de reglas simples pero efectivas para manipular y combinar números con signos. Estas reglas nos permiten simplificar expresiones y ecuaciones, haciendo que los problemas matemáticos sean más manejables. La clave de esta ley radica en comprender cómo interactúan los signos positivos y negativos al realizar operaciones matemáticas.
Reglas Fundamentales de la Ley de los Signos
A continuación, desglosaremos las reglas clave de la Ley de los Signos:
- Regla 1: Multiplicación y División - Cuando multiplicas o divides dos números con signos, el resultado sigue la siguiente regla: Si los signos son iguales, el resultado es positivo; si los signos son diferentes, el resultado es negativo.
- Regla 2: Suma y Resta - En la suma y resta de números con signos, la regla es similar: Si los signos son iguales, el resultado es positivo; si los signos son diferentes, restas los números y conservas el signo del número mayor.
- Regla 3: Signos de Exponentes - Al trabajar con exponentes, un signo negativo delante del exponente cambia el signo del resultado. Por ejemplo, (-2)^3 es igual a -8, mientras que (2)^-3 es igual a 1⁄8.
Estas reglas simples son la base para resolver una amplia gama de problemas matemáticos. Al aplicar la Ley de los Signos de manera consistente, podemos simplificar expresiones complejas y encontrar soluciones precisas.
Aplicación Práctica: Ejemplos y Ejercicios
Para ilustrar la aplicación de la Ley de los Signos, veamos algunos ejemplos prácticos:
| Ejercicio | Solución |
|---|---|
| (-5) * 3 | El resultado es -15, ya que los signos son diferentes. |
| 2 / (-4) | -0.5, porque al dividir dos números con signos diferentes, el resultado es negativo. |
| (-3) + 5 - (-2) | Sumando los números con signos iguales y restando el número con signo diferente, obtenemos 4. |
| (-2)^2 | El resultado es 4, ya que el exponente es positivo y el signo original se mantiene. |

Estos ejemplos demuestran cómo la Ley de los Signos nos permite manipular expresiones y obtener resultados precisos. Con la práctica, estas reglas se convierten en una herramienta intuitiva para resolver problemas algebraicos.
La Ley de los Signos en Acción: Casos Reales

La Ley de los Signos no solo es útil en ejercicios matemáticos, sino que también tiene aplicaciones prácticas en la vida real. Por ejemplo, en finanzas, se utiliza para calcular ganancias y pérdidas, especialmente en transacciones con valores positivos y negativos. En la programación, es esencial para manipular datos numéricos con signos.
Un caso real de aplicación de la Ley de los Signos es en la industria de la construcción. Los ingenieros y arquitectos utilizan esta ley para calcular las fuerzas y desplazamientos en estructuras, donde se trabajan con fuerzas positivas y negativas.
Ventajas de Dominar la Ley de los Signos
- Simplificación de Problemas - La Ley de los Signos nos permite simplificar expresiones complejas, haciendo que los problemas matemáticos sean más accesibles y comprensibles.
- Precisión en los Resultados - Al seguir las reglas de la Ley de los Signos, podemos asegurar que nuestros cálculos sean exactos y confiables.
- Eficiencia en la Resolución - Con la práctica, la aplicación de estas reglas se vuelve automática, lo que acelera la resolución de problemas.
Dominar la Ley de los Signos es una habilidad valiosa para cualquier estudiante o profesional en campos que involucren matemáticas y ciencias. Al comprender y aplicar estas reglas, podemos abordar problemas matemáticos con confianza y precisión.
Conclusión: La Ley de los Signos, una Herramienta Indispensable
La Ley de los Signos es una herramienta fundamental en el mundo de la matemática. Nos permite navegar con facilidad a través de operaciones que involucran signos positivos y negativos, asegurando que nuestros cálculos sean precisos y consistentes. Al comprender y aplicar estas reglas, podemos resolver problemas complejos y simplificar expresiones matemáticas.
A medida que exploramos más profundamente el mundo de las matemáticas, la Ley de los Signos sigue siendo una base sólida para avanzar en áreas más avanzadas de álgebra y análisis matemático. Con la práctica y la aplicación constante, esta ley se convierte en una herramienta intuitiva y poderosa para resolver problemas matemáticos.
¿Cuál es la importancia de la Ley de los Signos en matemáticas?
+La Ley de los Signos es fundamental en matemáticas porque nos brinda un conjunto de reglas claras para trabajar con números positivos y negativos. Esto nos permite simplificar expresiones y ecuaciones, haciendo que los problemas sean más manejables y sus soluciones más precisas.
¿Cómo se aplica la Ley de los Signos en la vida real?
+La Ley de los Signos tiene aplicaciones prácticas en áreas como las finanzas, donde se utiliza para calcular ganancias y pérdidas, y en la programación, para manipular datos numéricos. En la industria de la construcción, es esencial para calcular fuerzas y desplazamientos en estructuras.
¿Puedo aprender la Ley de los Signos rápidamente?
+Sí, con práctica y dedicación, la Ley de los Signos se vuelve una herramienta intuitiva. Al comprender las reglas básicas y aplicarlas consistentemente, puedes dominar esta ley en un corto período de tiempo.



