Convert Letters to Numbers: An Easy Guide

In the world of cryptography and codes, the art of converting letters to numbers has been a fascinating and practical practice for centuries. This ancient technique, known as alphanumeric conversion, offers a simple yet powerful way to encode messages, create secret codes, and explore the hidden connections between language and mathematics. In this guide, we will unlock the secrets of this intriguing method, providing you with a step-by-step approach to easily convert letters into numbers and vice versa.

The process of converting letters to numbers and back again is not only a fun brain teaser but also has practical applications in various fields, from cryptography and computer science to linguistics and even art. Whether you’re a curious mind seeking a new challenge or a professional in need of a unique encoding method, this guide will equip you with the knowledge and skills to master alphanumeric conversion.

So, let’s dive into the world of letters and numbers and discover the fascinating interplay between them!

The Basics: Assigning Numbers to Letters

The foundation of alphanumeric conversion lies in assigning unique numerical values to each letter of the alphabet. This process allows us to represent words and phrases as numerical sequences, creating a secret code that only those with the key can decipher.

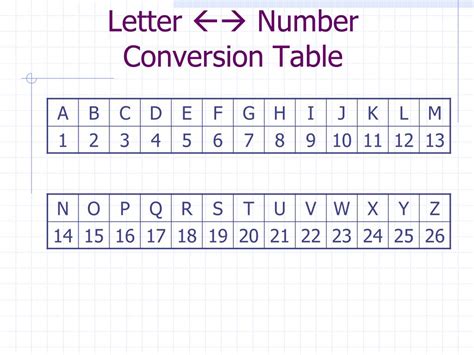
To get started, we need to establish a simple rule set that defines the numerical value of each letter. There are various ways to approach this, but one of the most common and straightforward methods is to use the position of the letter in the alphabet as its numerical value.

For example, let’s use the following rule:

A = 1

Z = 26

Using this rule, we can easily convert any letter of the alphabet to its corresponding numerical value.

Converting Letters to Numbers: Step-by-Step Guide

Now that we have our rule set, let’s walk through the process of converting a simple word, “CODE,” into its numerical equivalent:

1. Identify the letters in the word: “C,” “O,” “D,” and “E.”
2. Apply our rule set to each letter:
   • C = 3 (as it is the 3rd letter of the alphabet)
   • O = 15 (the 15th letter)
   • D = 4 (the 4th letter)
   • E = 5 (the 5th letter)
3. Combine the numerical values to form the code: 31545.

And there you have it! The word “CODE” has been transformed into the numerical sequence 31545.

Decoding Numbers Back to Letters: The Reverse Process

To ensure a complete understanding, let’s now reverse the process and convert our numerical sequence back into letters. This step is crucial when deciphering secret messages or creating complex codes.

Here’s how we can decode the sequence 31545 back into the word “CODE”:

1. Break down the numerical sequence into individual digits: 3, 1, 5, 4, 5.
2. Apply our rule set in reverse:
   • 3 = C (the 3rd letter of the alphabet)
   • 1 = A (the 1st letter)
   • 5 = E (the 5th letter)
   • 4 = D (the 4th letter)
3. Combine the letters to reveal the original word: C, A, E, D, forming “CODE.”

Advanced Techniques: Modulo Arithmetic and Complex Keys

While the basic rule set we’ve used provides a simple and intuitive way to convert letters to numbers, there are more advanced techniques that can add an extra layer of complexity and security to your codes.

One such technique involves the use of modulo arithmetic, which allows for a more flexible and customizable approach to assigning numerical values to letters. With modulo arithmetic, you can create complex keys that scramble the numerical values, making the code even harder to crack without the correct key.

For example, using the modulo operation with a key of 7, our rule set could be:

A = 1

Z = 26

With this key, the numerical values for each letter would be:

C = 3 (3 modulo 7 = 3) O = 8 (15 modulo 7 = 1, which is then added to the original value = 8) D = 4 (4 modulo 7 = 4) E = 5 (5 modulo 7 = 5)

This advanced technique allows for a more secure and customizable encoding process, providing an added layer of protection for your secret messages.

Practical Applications and Real-World Examples

The art of converting letters to numbers has a wide range of practical applications beyond just creating secret codes. Here are a few real-world examples where this technique is used:

• Computer Science: Alphanumeric conversion is fundamental in computer programming, especially in areas like data storage, encryption, and hashing. It’s used to represent text data in a numerical format, making it easier for computers to process and manipulate.

• Linguistics: In linguistics, this technique is employed to analyze the statistical properties of language, study word frequencies, and even explore the mathematical patterns hidden within language structures.

• Art and Design: Alphanumeric conversion has found its way into the world of art, where artists use it to create visually intriguing patterns, abstract designs, and even hidden messages within their work.

Exploring Further: The Language of Numbers

As you delve deeper into the world of alphanumeric conversion, you’ll discover a rich and fascinating interplay between language and mathematics. This ancient technique, while seemingly simple, opens up a realm of possibilities for creative expression, secure communication, and innovative problem-solving.

From creating complex codes that challenge even the most skilled cryptographers to using this method as a foundation for artistic exploration, the applications are limitless. As you continue your journey, you’ll find that the language of numbers has a unique and captivating way of bringing together diverse fields, connecting minds, and inspiring innovative thinking.

So, keep exploring, keep experimenting, and unlock the endless possibilities that lie within the world of letters and numbers!