Unveiling the Laplace Transform Formula Sheet
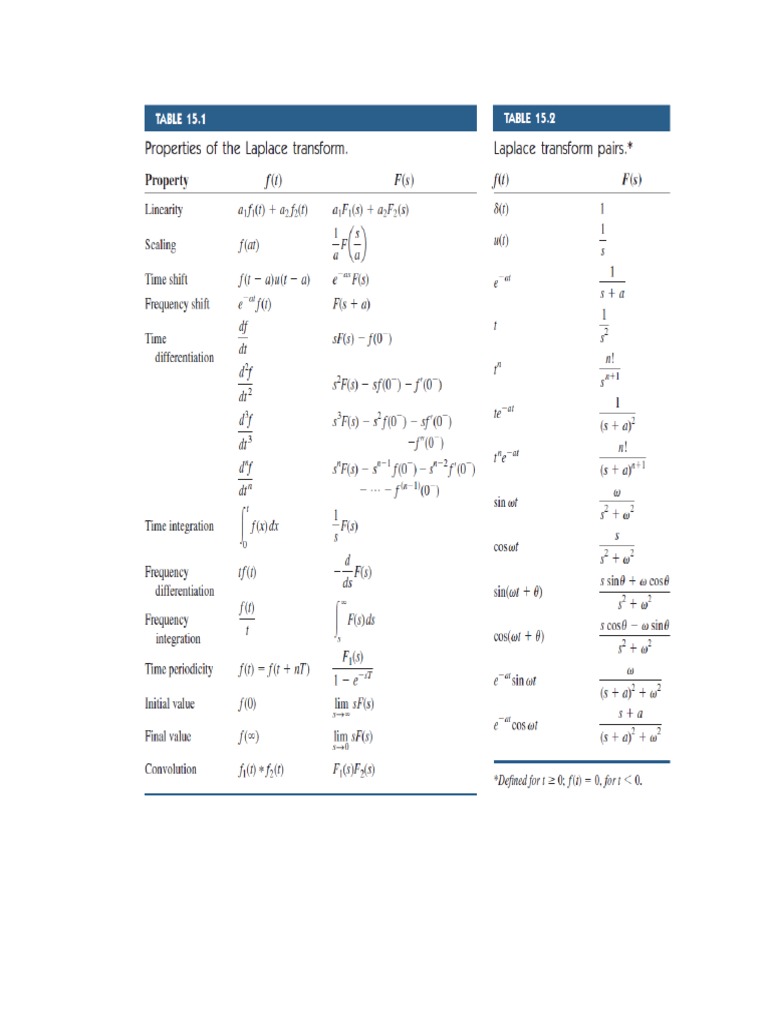
The Laplace transform is a powerful mathematical tool that has revolutionized the field of engineering and scientific analysis. It provides a means to transform complex functions and equations into a new domain, offering a fresh perspective and simplifying many intricate problems. In this comprehensive guide, we delve into the intricacies of the Laplace transform formula sheet, exploring its core principles, practical applications, and the profound impact it has on various disciplines.
At its core, the Laplace transform is a mathematical operation that maps a function of a real variable, typically time, to a function of a complex variable. This transformation involves integrating the original function multiplied by an exponential decay factor, over the entire real axis. The resulting function, known as the Laplace transform, provides a unique representation of the original function in the complex plane.
The beauty of the Laplace transform lies in its ability to transform differential equations, integral equations, and other mathematical constructs into algebraic equations. This transformation simplifies the analysis and solution of complex problems, especially in areas such as signal processing, control systems, electrical engineering, and physics. By converting time-domain problems into the frequency domain, the Laplace transform reveals hidden patterns, simplifies calculations, and provides a powerful framework for understanding and manipulating dynamic systems.
To fully grasp the potential of the Laplace transform, it is essential to familiarize oneself with the fundamental formulas and properties that underpin this mathematical tool. Let’s delve into the core concepts and explore the practical applications of the Laplace transform formula sheet.
Understanding the Laplace Transform
The Laplace transform is defined for a function f(t) as:
\[ \begin{equation*} \mathcal{L}\{f(t)\} = F(s) = \int_0^{\infty} e^{-st} f(t) \, dt \, . \end{equation*} \]
In this formula, f(t) represents the original function, F(s) is the Laplace transform, and s is a complex variable that acts as the transformation parameter. The exponential decay factor, e^{-st}, ensures that the integral converges and allows for the transformation of the function into the complex plane.
The inverse Laplace transform, which maps a function of a complex variable back to the time domain, is given by:
\[ \begin{equation*} \mathcal{L}^{-1}\{F(s)\} = f(t) = \frac{1}{2\pi i} \int_{\gamma - i\infty}^{\gamma + i\infty} e^{st} F(s) \, ds \, . \end{equation*} \]
Here, \gamma is a real number that determines the contour of integration, and i is the imaginary unit. The inverse Laplace transform allows us to retrieve the original function from its Laplace transform representation.
Key Properties and Formulas
The Laplace transform possesses a set of fundamental properties and formulas that make it an invaluable tool for mathematical analysis. Some of these key properties include:
Linearity: The Laplace transform is a linear operator, meaning it distributes over addition and scalar multiplication. This property allows for easy manipulation and combination of functions.
Time Shifting: Shifting a function in time results in a simple modification of its Laplace transform. If f(t) is shifted by a constant t_0, its Laplace transform becomes e^{-st_0}F(s).
Time Scaling: Scaling a function in time also affects its Laplace transform. If f(t) is scaled by a factor a, its Laplace transform becomes \frac{1}{a}F(\frac{s}{a}).
Convolution: The convolution of two functions, f(t) and g(t), has a particularly elegant representation in the Laplace domain. The convolution theorem states that the Laplace transform of the convolution of two functions is equal to the product of their individual Laplace transforms.
\[ \begin{equation*} \mathcal{L}\{f(t) * g(t)\} = F(s)G(s) \, . \end{equation*} \]
Initial and Final Value Theorems: These theorems provide insights into the behavior of a system at its initial and final states. The initial value theorem states that the Laplace transform of a function at s = 0 gives the initial value of the function, while the final value theorem gives the final value of the function as s \rightarrow \infty.
Poles and Zeros: The Laplace transform of a function is a rational function of s, and its poles and zeros provide important information about the behavior of the system. Poles correspond to exponential modes in the time domain, while zeros represent damping factors.
Practical Applications
The Laplace transform finds extensive applications in various fields, particularly in control systems, signal processing, and electrical engineering. Here are some key areas where the Laplace transform is indispensable:
Control Systems: The Laplace transform is the backbone of control system analysis. It allows engineers to model and analyze complex systems, design controllers, and study the stability and performance of feedback control loops. By transforming differential equations into algebraic equations, the Laplace transform simplifies the design and optimization of control systems.
Signal Processing: In signal processing, the Laplace transform is used to analyze and manipulate signals in the frequency domain. It enables the extraction of key features, filtering, and modulation of signals. The transform’s ability to represent signals in the frequency domain provides valuable insights for applications such as audio processing, image analysis, and telecommunications.
Electrical Engineering: The Laplace transform is an essential tool in electrical engineering for analyzing and designing electrical circuits. It simplifies the analysis of transient responses, impedance, and frequency response characteristics of circuits. The transform also plays a crucial role in power systems analysis and control.
Physics and Engineering: The Laplace transform finds applications in a wide range of physical and engineering problems. It is used in heat transfer analysis, fluid dynamics, and vibration analysis. In these fields, the transform provides a powerful means to solve differential equations and understand the behavior of dynamic systems.
Case Study: Control Systems Analysis
To illustrate the practical application of the Laplace transform, let’s consider a simple example from control systems. Suppose we have a mass-spring-damper system, where a mass is attached to a spring and a damper. The system is governed by the following differential equation:
\[ \begin{equation*} m\ddot{x} + c\dot{x} + kx = F(t) \, , \end{equation*} \]
where m is the mass, c is the damping coefficient, k is the spring constant, F(t) is the applied force, and x(t) is the displacement of the mass. To analyze the system’s response, we can apply the Laplace transform to both sides of the equation.
By taking the Laplace transform of the differential equation, we obtain:
\[ \begin{align*} m(s^2X(s) - sx(0) - \dot{x}(0)) + csX(s) + kX(s) &= F(s) \\ (ms^2 + cs + k)X(s) &= F(s) + msx(0) + m\dot{x}(0) \, . \end{align*} \]
Here, X(s) is the Laplace transform of x(t), and F(s) is the Laplace transform of the applied force. This algebraic equation represents the transfer function of the system, which describes the relationship between the input force and the system’s response.
The transfer function allows us to analyze the system’s stability, frequency response, and other important characteristics. By performing calculations and manipulations in the Laplace domain, we can gain valuable insights into the system’s behavior without the need for complex differential equation solving.
Future Trends and Extensions
The Laplace transform has already proven its worth in numerous applications, but its potential is far from exhausted. Ongoing research and developments continue to expand its reach and applicability. Here are some future trends and extensions to explore:
Fractional Calculus: The Laplace transform is closely related to fractional calculus, which extends the concept of derivatives and integrals to non-integer orders. Fractional Laplace transforms offer new perspectives and solutions to problems involving anomalous diffusion, viscoelastic materials, and fractional order systems.
Generalized Functions: The Laplace transform can be generalized to work with distributions and generalized functions, allowing for the analysis of more complex and singular functions. This extension broadens the scope of problems that can be tackled using the Laplace transform.
Multidimensional Laplace Transforms: While the Laplace transform is typically applied to one-dimensional functions, extensions to higher dimensions, such as the multidimensional Laplace transform, provide powerful tools for analyzing multi-variable systems and problems in image processing and physics.
Hybrid Transforms: Combining the Laplace transform with other transforms, such as the Fourier transform or wavelet transforms, can lead to hybrid transforms that offer enhanced capabilities for signal processing and analysis. These hybrid transforms provide a unified framework for solving complex problems.
In conclusion, the Laplace transform formula sheet is a powerful resource for engineers, scientists, and mathematicians. Its ability to transform functions and equations into a new domain opens up a world of possibilities for analysis and problem-solving. From control systems to signal processing and beyond, the Laplace transform continues to shape our understanding of dynamic systems and drive innovation in various fields. By mastering the concepts and formulas presented here, one can unlock the full potential of this mathematical tool and tackle complex problems with elegance and precision.