The Karnaugh Map Simplified

An Intuitive Guide to Mastery

The Karnaugh map, often referred to as a K-map, is a powerful tool in the field of digital electronics and Boolean algebra. It provides a systematic and visual way to simplify and optimize Boolean expressions, making complex logic circuits more manageable. Mastering this technique is crucial for engineers and designers working with digital systems, as it enables efficient design, optimization, and minimization of logic circuits. In this article, we will embark on a journey to demystify the Karnaugh map, breaking down its principles and offering practical insights to enhance your understanding and application.

Understanding the Basics: A Step-by-Step Introduction

The Concept of a Karnaugh Map: At its core, a Karnaugh map is a graphical representation of a truth table. It organizes variables and their combinations in a way that simplifies the process of identifying and grouping adjacent 1’s, making it easier to apply the principles of Boolean algebra for minimization.

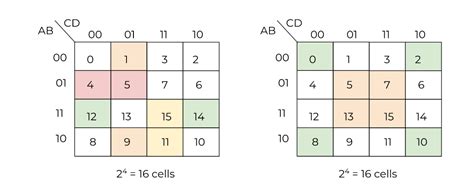
Step 1: Constructing the Map Begin by creating a square grid, with each cell representing a unique combination of input variables. The number of cells depends on the number of variables. For example, with two variables (A and B), you’ll have a 2x2 grid, and with three variables (A, B, and C), it becomes a 2x2x2 grid, and so on.

Step 2: Populating the Map Next, assign each cell a specific variable combination, following a consistent pattern. This pattern ensures that adjacent cells differ by only one variable, which is crucial for the simplification process. For instance, with two variables (A and B), the top-left cell would represent A=0 and B=0, the top-right cell would be A=1 and B=0, the bottom-left cell would be A=0 and B=1, and the bottom-right cell would be A=1 and B=1.

Step 3: Filling the Map with Truth Values Once the map is constructed and populated, fill each cell with the corresponding truth value from the original Boolean expression or truth table. For example, if the expression is A + B, the cells representing A=1 and B=1 would be filled with 1’s, while the rest would be 0’s.

Step 4: Simplifying with Adjacency The key to simplification lies in grouping adjacent 1’s. Look for groups of 1’s that form a rectangle or square (referred to as ‘adjacent’ in K-map terminology). Each group represents a term in the simplified Boolean expression. For instance, a group of 1’s in the top-left and bottom-right cells would represent the term AB, as both A and B are high in these cells.

Step 5: Constructing the Simplified Expression Each group of adjacent 1’s represents a term in the simplified expression. Combine these terms to form the final, minimized Boolean expression.

The Art of Simplification: Strategies and Tips

Group Size Matters: Always aim for the largest possible groups of adjacent 1’s. This reduces the number of terms in the simplified expression, making the circuit more efficient.

Corner Cells: Corner cells in the K-map often represent ‘don’t care’ conditions. These cells can be ignored in the simplification process, as they don’t affect the final result.

Symmetry and Pattern Recognition: Look for patterns and symmetries in the K-map. This can help identify groups of 1’s more efficiently, especially in larger maps.

Don’t Overlook Single 1’s: Even single 1’s can represent a term in the simplified expression. Make sure to account for these in your final equation.

Advanced Techniques: Beyond the Basics

Don’t Care Conditions: In some cases, you might have additional information about ‘don’t care’ conditions. These are values of the input variables that will never occur in the circuit’s operation. By knowing these conditions, you can strategically place 1’s or 0’s in the K-map to aid in simplification.

Gray Code Ordering: In certain situations, it’s beneficial to arrange the cells in Gray code order. This ensures that adjacent cells differ by only one bit, which can simplify the process of identifying adjacent 1’s.

Multiple Levels of Variables: For more complex scenarios with multiple levels of variables, you might need to create a multi-level K-map. This involves creating a 3D map, where each layer represents a different variable level.

Practical Application: A Real-World Example

Let’s consider a practical scenario: designing a logic circuit to control a traffic light system. The circuit needs to manage the green, yellow, and red lights based on a set of input conditions. By using a Karnaugh map, we can efficiently minimize the Boolean expressions for each light, leading to a more optimized and cost-effective circuit design.

Final Thoughts and Takeaways

The Karnaugh map is a versatile and powerful tool in the digital electronics designer’s toolkit. By understanding its principles and applying them with precision, you can simplify complex Boolean expressions, optimize logic circuits, and ultimately enhance the efficiency and performance of digital systems.