Rectangles and Rhombuses: What's the Connection?
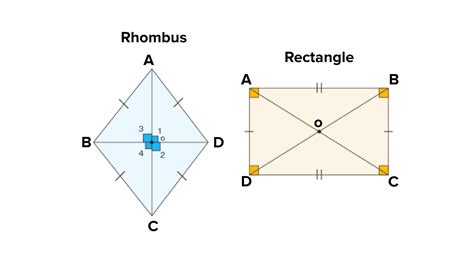
Rectangles and rhombuses may seem like distinct shapes, but they share an intriguing connection, especially in the world of geometry. While a rectangle is characterized by its four right angles and equal opposite sides, a rhombus, often overlooked as a simple diamond shape, possesses a unique set of attributes that bring it closer to the rectangle family than one might initially think.
The secret lies in the definition of these shapes and how they relate to each other through shared properties. This article will explore the fundamental traits of rectangles and rhombuses, delve into their shared characteristics, and discuss the implications of their mathematical kinship.
Understanding Rectangles

Rectangles are one of the most familiar shapes in geometry. Their defining features include four right angles and two pairs of parallel and congruent sides. This means that the opposite sides of a rectangle are always equal in length and run parallel to each other.
The mathematical equation for the area of a rectangle is straightforward: Area = length × width. This simplicity is one of the reasons rectangles are so commonly used in architecture, design, and everyday life. They provide a stable, reliable shape that is easy to work with mathematically and visually.
Exploring Rhombuses

A rhombus, on the other hand, is a less commonly discussed shape. It is defined as a quadrilateral with all four sides of equal length. This means that, unlike a rectangle, a rhombus does not necessarily have right angles. Instead, the focus is on the congruence of its sides.
The area of a rhombus is calculated using a different formula: Area = ½ × product of its diagonals. This formula reveals an interesting connection between rhombuses and circles, as the area of a circle can also be calculated using its radius.
Shared Characteristics: The Common Ground
The connection between rectangles and rhombuses becomes apparent when we examine their shared characteristics.
Symmetry
Both rectangles and rhombuses exhibit a high degree of symmetry. Rectangles have two lines of symmetry: one through each diagonal. Rhombuses, similarly, have two lines of symmetry: one through each of its diagonals. This shared symmetry is a crucial aspect that ties these shapes together.
Parallel Sides
Despite the lack of right angles, rhombuses still possess parallel sides. This is a fundamental characteristic that connects them to rectangles. In fact, a rhombus can be seen as a special case of a rectangle where all sides are equal, creating a diamond-like shape.
Area Calculation
The area calculation for both shapes, while different, shares a common denominator: the length of their sides. For rectangles, the area is simply the product of the length and width. For rhombuses, the area is determined by the product of its diagonals, which are effectively the length of its sides in a different orientation.
The Mathematical Implication
The shared characteristics between rectangles and rhombuses have a profound mathematical implication. It demonstrates that, despite their apparent differences, these shapes are part of a broader family of quadrilaterals with similar underlying properties.
This connection is not limited to rectangles and rhombuses. It extends to other shapes like squares, parallelograms, and even trapezoids, each with its unique set of attributes but all sharing fundamental characteristics that tie them to this broader family.
Practical Applications
Understanding the connection between rectangles and rhombuses has practical applications in various fields. In architecture and design, for instance, recognizing the flexibility of these shapes can lead to innovative solutions. A designer might start with a rhombus and, by understanding its connection to the rectangle, manipulate its angles and sides to create a unique and visually appealing structure.
In the world of computer graphics and animation, this understanding can simplify the coding and rendering of shapes. By recognizing the underlying mathematical relationships, developers can create efficient algorithms to generate and manipulate these shapes, leading to smoother and more realistic animations.
Conclusion: A Surprising Kinship
In conclusion, rectangles and rhombuses, while seemingly distinct, share a surprising kinship. Their shared characteristics, from symmetry to parallel sides and even area calculation, demonstrate a fundamental connection that ties them to a broader family of quadrilaterals.
This connection is a testament to the elegance and interconnectedness of mathematical concepts. It shows that, even in seemingly disparate shapes, there are underlying principles that unite them, providing a deeper understanding of the world around us.
So, the next time you encounter a rectangle or a rhombus, remember the surprising kinship that binds them together, and appreciate the intricate web of relationships that exist in the world of geometry.